Связь между трением, теплоотдачей и диффузией. Тройная аналогия, страница 9

Найденное решение применимо для продольного обтекания плоской пластины даже в том случае, когда отсос начинается непосредственно с передней кромки. В самом деле, здесь толщина пограничного слоя на передней кромке равна нулю. Вниз по течению она начинает расти и достигает своего значения, определяемого формулами (2.120). Распределение скоростей имеет простой вид (2.119) только после того, как течением будет пройден вдоль пластины некоторый начальный участок. Как было показано при исследовании течения на начальном участке [1], автомодельное (асимптотическое) распределение скоростей (2.119) устанавливается со значений продольной координаты х:

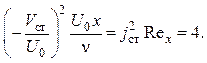                          (2.123)

Аналогичным образом можно получить автомодельное решение уравнения энергии. А можно, воспользовавшись аналогией Рейнольдса, сразу записать выражение для коэффициента теплообмена

                         (2.124)

Пограничный слой с вдувом

Для многих прикладных задач представляет интерес случай вдува через поверхность теплообмена (пористое охлаждение, испарение, сублимация, химически реагирующая поверхность и т.д.). Анализ точных решений уравнений пограничного слоя на проницаемой поверхности [1, 2] показывает, что автомодельные решения существуют, когда вдув газа по длине изменяется в соответствии с соотношением

                                     (2.125)

при U₀ = cx^m. В частности, в окрестности лобовой точки (m = 1) V_ст = const. При обтекании плоской пластины (m = 0)  Из результатов расчетов следует, что вдув газа в пограничный слой приводит к резкому снижению коэффициентов трения и тепломассообмена. При этом профили скоростей, температур и концентраций в пограничном слое деформируются таким образом, что градиенты этих величин у стенки резко уменьшаются.

В качестве примера на рис. 2.10 показано изменение профиля скорости в зависимости от интенсивности вдува. Профили  температур и концентраций при Pr = Sc = 1 совпадают с профилем скорости, а при Pr ≠ 1 несколько отличаются. Анализ рассчитанных профилей   скорости,   температур  и  концентраций  обнаруживает, что с ростом параметра вдува пограничный слой утолщается, а при достижении значений скорости вдува V_ст :

                              (2.126)

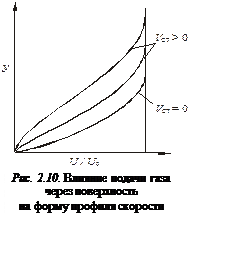происходит оттеснение пограничного слоя от поверхности, что характеризуется равенством нулю касательного напряжения на поверхности (или коэффициента трения), теплового и диффузионного потоков (или коэффициентов тепломассообмена).

Так как коэффициент трения на непроницаемой пластине обусловлен известным соотношением

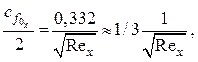
то можно ввести еще параметр вдува, вычисляемый по  коэффициенту трения на непроницаемой пластине:

                      (2.127)

Здесь везде индекс х указывает на то, что значения этих параметров определяются по текущей длине х или по Re_x. Тогда в соответствии с соотношением (2.126) ламинарный пограничный слой оттесняется от стенки, и коэффициенты тепломассообмена и трения становятся равными нулю при

          (2.128)

При анализе ламинарного пограничного слоя на проницаемой стенке можно воспользоваться и методом Кармана – Польгаузена, когда профиль скорости аппроксимируется степенным полиномом с учетом граничных условий. Однако, как показано некоторыми исследователями, в режимах сильного вдува имеется значительное расхождение с результатами точного решения, и этот метод не дает конечного значения критического параметра вдува, а  при .

Пленочная теория

Довольно широкое распространение получили работы, основанные на использовании пленочной модели течения на проницаемой поверхности. В пленочной теории принимается допущение о том, что можно пренебречь изменением параметров в направлении течения по сравнению с изменением в поперечном направлении:  Физически это означает, что действительный двумерный пограничный слой заменяется одномерным течением Куэтта. В соответствии с принятым допущением запишем уравнения сохранения:

– массы

                         (2.129)

– количества движения

                               (2.130)

– энергии

                                     (2.131)

Граничные условия:

– при   у = 0:     U = 0,      T = T_ст;