Асимптотическая теория турбулентного пограничного слоя

	Q

 

Г л а в а   4

      АСИМПТОТИЧЕСКАЯ ТЕОРИЯ ТУРБУЛЕНТНОГО

       ПОГРАНИЧНОГО СЛОЯ

4.1.  Предельные относительные законы трения

        и тепломассообмена

	ТВ

           очное  решение  системы  дифференциальных  уравнений

           пограничного слоя возможно лишь для ограниченного круга задач. Использование численных методов громоздко и трудоемко.

Поэтому большое значение приобретают приближенные методы решения, основанные на применении интегральных уравнений импульсов, энергии и диффузии. Их получают в результате интегрирования дифференциальных уравнений по толщине пограничного слоя.

Важной особенностью интегральных уравнений является то, что они выведены без каких-либо физических допущений и справедливы как для ламинарного, так и для турбулентного пограничных слоев, а также для переходной области течения. Они применимы и для «стандартных» условий течения, и для течений, осложненных воздействием возмущающих факторов: неизотермичности, сжимаемости, вдува газа со стенки, наличия химических реакций и т. п.

Интегральные уравнения имеют вид:

·  уравнение импульсов

;                 (4.1)

·  уравнение энергии

;                        (4.2)

·  уравнение диффузии

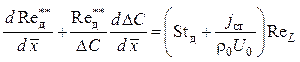 .                 (4.3)

Здесь  ,    ,    ,

,  ,

     ,    ,  ,

,   ,    ,

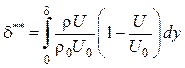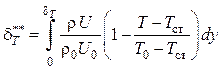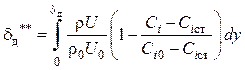.                           (4.4)

Чтобы решить эти уравнения, необходимо знать законы трения, тепло-обмена и массообмена. В общем случае . Для ламинарного режима течения при определенных граничных условиях законы можно определить аналитическим путем. Для турбулентного режима их получают на основе полуэмпирических теорий турбулентности.

Наиболее простой и результативной является так называемая «теория предельных относительных законов», разработанная С.С. Кутателадзе и А.И. Леонтьевым. Они показали, что при больших числах Рейнольдса (Re®¥) можно получить теоретические зависимости для относительных функций тепломассообмена и трения , , , которые не содержат эмпирических констант турбулентности и позволяют учесть влияние различных возмущающих факторов: неизотермичности, сжимаемости, вдува газа со стенки и др.

Интегральные уравнения, записанные через относительные функции Y, будут иметь вид (на примере уравнения энергии)

                ,                    (4.5)

где ,   – относительный параметр вдува.

St, St₀ – числа Стентона в реальных условиях течения и в стандартных (обтекание непроницаемой пластины дозвуковым безградиентным потоком в квазиизотермических условиях).

Для стандартных условий течения при турбулентном режиме:

.                                   (4.6)

Получим предельный относительный закон теплообмена. Вывод предельных законов трения и массообмена аналогичен, и приводить его не будем.

Физически существование предельных законов объясняется  тем, что с увеличением числа Re толщина вязкого подслоя убывает быстрее, чем толщина всего турбулентного слоя:

.

В ядре турбулентного пограничного слоя плотность теплового потока

 ,                                    (4.7)

где  – пульсации скорости в поперечном направлении; – пульсации температуры.

Связь пульсаций скорости  и температуры  c осредненными параметрами течения  и  определяется с использованием гипотезы Прандтля

                                ,       .                            (4.8)

Здесь  и  – длина динамического и теплового пути смешения – расстояние, на котором комок жидкости, перемещающийся при пульсации из одного слоя в другой, сохраняет составляющую импульса в направлении оси  и теплоту.

С учетом гипотезы Прандтля плотность теплового потока будет иметь вид

.                                   (4.9)

Считая, что длины динамического и теплового путей смешения равны, , имеем

.                                 (4.10)

Введем значения относительной плотности теплового потока

,      ,                               (4.11)

где   и   – значения теплового потока в данной точке пограничного слоя и на стенке в «стандартных» условиях течения (обтекание непроницаемой пластины дозвуковым безградиентным потоком в квазиизотермических условиях);  и  – то же в условиях, отличных от стандартных: воздействие различных возмущающих факторов – поперечного потока вещества, сжимаемости, неизотермичности и др.

Из (4.11) с учетом (4.10) можно записать тепловой поток на стенке:

.                              (4.12)

Делим левую и правую части уравнения (4.12) на  и введем безразмерные параметры  ,  ,  :

.     (4.13)

Используя подобие профилей скорости и температуры в виде

, имеем

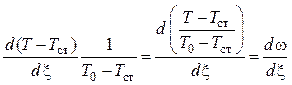.              (4.14)

Тогда из (4.13) с учетом того, что

, имеем

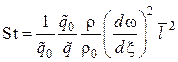.                               (4.15)

Представим число Стентона в относительном виде. Разделим левую и правую части (4.15) на :

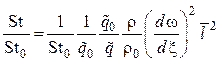.                        (4.16)