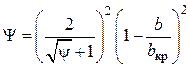 ,
(4.73)
,
(4.73)
где ![]() определяется
по (4.71) и (4.72).
определяется
по (4.71) и (4.72).
При вдуве инородного газа через проницаемую пластину
для рас-сматриваемых условий (![]()
![]() ) должно
существовать подобие в распределении энтальпий, скоростей и массовых
концентраций:
) должно
существовать подобие в распределении энтальпий, скоростей и массовых
концентраций:
![]() .
(4.74)
.
(4.74)
Распределение плотности в пограничном слое в предельном интеграле при вдуве инородного газа будет иметь вид:
![]() .
.
Температуру ![]() найдем
из подобия (4.74):
найдем
из подобия (4.74):
![]() .
(4.75)
.
(4.75)
Считая, что теплоемкость смеси газов ![]() в
рассматриваемом диапазоне температур не изменяется
в
рассматриваемом диапазоне температур не изменяется
![]() ,
,
определим температуру газа в рассматриваемой точке пограничного слоя
![]() .
(4.76)
.
(4.76)
Рассмотрим двухкомпонентный газ. Найдем теплоемкость смеси газов в данной точке пограничного слоя
![]() ,
(4.77)
,
(4.77)
где С¢ и ![]() –
массовые концентрации охладителя (вдуваемого газа) и газа основного потока в
данной точке пограничного слоя;
–
массовые концентрации охладителя (вдуваемого газа) и газа основного потока в
данной точке пограничного слоя; ![]() и
и
![]() – их
теплоемкости.
– их
теплоемкости.
Концентрации ![]() и
и ![]() определим из
условия подобия (4.74)
определим из
условия подобия (4.74)
![]() ,
,
![]() .
.
Тогда из (4.77) с учетом предыдущих выражений для концентраций после преобразований будем иметь
![]() .
.
И окончательно выражение для теплоемкости смеси газов примет вид
![]() .
(4.78)
.
(4.78)
Подставляя (4.78) в (4.76), получаем выражение для температуры
![]() .
(4.79)
.
(4.79)
Найдем молекулярную массу смеси газов ![]() в рассматриваемой
точке пограничного слоя.
в рассматриваемой
точке пограничного слоя.
![]() .
(4.80)
.
(4.80)
Из подобия профилей концентраций и скоростей с учетом того, что ![]() , имеем
, имеем
![]() .
(4.81)
.
(4.81)
Подставим (4.81) в (4.80):
![]() .
.
![]()
![]() ,
,
так как
![]() ,
,
![]() .
.
Найдем распределение плотности смеси газов в пограничном слое:
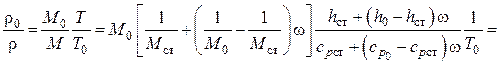
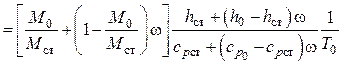 .
.
Обозначим
![]() ,
, ![]() ,
, ![]() ,
,
тогда
![]() .
.
Для газов одинаковой атомности
![]() ,
,
![]() , или
, или ![]() , т. е.
, т. е. ![]() .
.
Тогда
![]() ,
,
т. е. если при инородном вдуве вместо температуры использовать энтальпию, то распределение плотности будет иметь такой же вид, как и при однородном вдуве [см. уравнение (4.67)]. Тогда и выражения для относительной функции теплообмена и критического параметра вдува также будут иметь прежний вид [уравнения (4.69)–(4.72)].
Влияние вдува инородного газа на коэффициент трения на пластине показано на рис. 4.5.
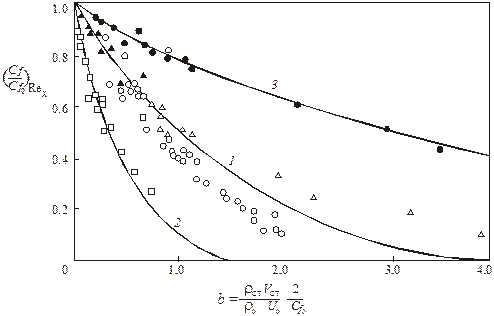
Рис. 4.5. Влияние вдува инородного газа на коэффициент трения
на пластине: 1 – вдув воздуха в воздух; 2 – гелий – воздух;
3 – фреон-12 – воздух. Точки – опыты
О Т С О С
Отсос газа из пограничного слоя может использоваться для интенсификации процессов тепломассообмена, для повышения устойчивости течения. Процессы, аналогичные отсосу, имеют место при конденсации, адсорбции.
Параметр проницаемости стенки при отсосе по сравнению с вдувом имеет
отрицательное значение, так как поток массы направлен к стенке ![]() .
.
Относительная функция трения (или теплообмена) будет иметь вид:
![]() .
.
Профиль скорости в пограничном слое при отсосе:
![]() ,
,
где ![]() –
распределение скорости в пограничном слое на непроницаемой пластине.
–
распределение скорости в пограничном слое на непроницаемой пластине.
Для предельного отсоса газа ![]() и
и
![]() ,
, ![]()
![]() .
.
Таким образом, при отсосе турбулентного слоя существует предельное решение. Аналогичный результат, как будет показано ниже, получается и для случая асимптотического отсоса.
Автомодельное решение для асимптотического отсоса
![]()
![]() .
.
Уравнение движения вблизи стенки
![]() ,
, ![]() ,
, ![]() при
при ![]() .
.
Распределение скорости в пограничном слое имеет вид
![]() .
.
Тогда касательное напряжение
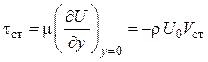 .
.
Коэффициент трения
![]() ,
, ![]() .
.
Предельный закон трения
![]() ,
, ![]() .
.
4.4. Расчет турбулентного пограничного слоя
на проницаемой поверхности
Начальными параметрами в расчете являются:
· координаты рассматриваемых поперечных
сечений (![]() ), которые
отсчитываются от передней кромки пористой пластины;
), которые
отсчитываются от передней кромки пористой пластины;
· параметры основного потока:
![]() –
энтальпия,
–
энтальпия,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.