Асимптотическая теория турбулентного пограничного слоя, страница 2

Учитывая, что ,  уравнение (4.16) имеет вид:

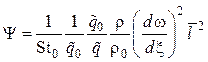.                          (4.17)

Преобразуем (4.17), разделяя переменные

.                            (4.18)

 .                      (4.19)

Выражение (4.19) справедливо для турбулентного ядра пограничного слоя от  (или ) до  1. Проинтегрируем (4.19):

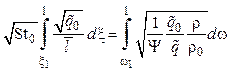.                  (4.20)

Поскольку при    , можно изменить нижние пределы интегрирования:

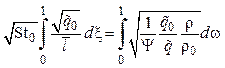.                     (4.21)

В ряде работ показано, что в пристенной области  и . Тогда в левой части выражения (4.21) стоят все члены, характеризующие «стандартные» условия, и они не зависят от возмущающих факторов. Поэтому уравнение (4.21) справедливо, в частности, и для «стандартных» условий. А для таких условий:

  и  ,   ,   ,  .

Тогда уравнение (4.21) имеет вид

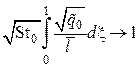    при       

независимо от наличия и вида возмущающих факторов.

Соответственно правая часть уравнения (4.21) также стремится к единице

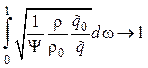   при      .

В результате получаем выражение для относительной функции теплообмена:

                                 ,

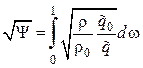или

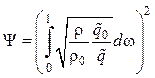 .                                 (4.22)

Полученная зависимость (4.22) представляет собой основной интеграл теории Кутателадзе–Леонтьева.

Как видно, для определения относительной функции теплообмена (или трения) необходимо знать распределение плотности газа  и теплового потока (или касательных напряжений ) по толщине пограничного слоя.

4.2.   Обтекание непроницаемой стенки.

         Влияние неизотермичности

         и сжимаемости газа

4.2.1. ВЛИЯНИЕ НЕИЗОТЕРМИЧНОСТИ НА ТЕПЛООБМЕН

 Рассмотрим турбулентный пограничный слой  газа на непроницаемой стенке. Как мы показали выше, предельный относительный закон теплообмена описывается формулой (4.22).

Поскольку стенка непроницаемая, распределение теплового потока поперек пограничного слоя ,   и уравнение (4.22) имеет вид

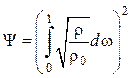   .                                     (4.23)

Определим влияние неизотермичности газа на теплообмен, когда температура газа сильно изменяется поперек пограничного слоя. При этом существенно меняется плотность газа внутри пограничного слоя, которая характеризует  в формуле (4.23).

Распределение плотности по сечению пограничного слоя найдем из уравнения газового состояния

                                   ,                                            (4.24)

где – газовая постоянная,  [Дж/кг×К].

Отсюда следует, что для однородного газа () отношение плотности в рассматриваемой точке пограничного слоя и на его внешней границе будет иметь вид

.                                          (4.25)

Распределение температуры внутри пограничного слоя получим из условия подобия полей скоростей и температур

.                                  (4.26)

Найдем из (4.26) отношение

,

.

Введем понятие температурного фактора (или фактора неизотермичности)

.

Тогда

.

Для однородного газа распределение плотности будет [из (4.25)]:

 .                               (4.27)

Подставляя (4.27) в (4.23), имеем

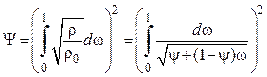.                    (4.28)

Проинтегрируем (4.28):

.

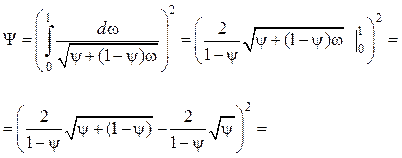
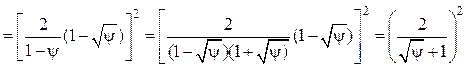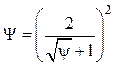.                                         (4.29)

Расчет влияния неизотермичности на теплообмен по формуле (4.29) показан на рис. 4.1.

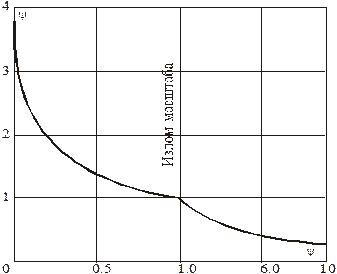
Рис. 4.1. Влияние неизотермичности

на теплообмен ()

4.2.2. Влияние сжимаемости (числа М) на теплообмен

 Предельный относительный закон теплообмена в условиях сжимаемости имеет вид уравнения (4.23), так как распределение плотности теплового потока при сверхзвуковом течении практически не меняется, т. е. остается таким же, как и в стандартных условиях, . Об этом свидетельствуют данные различных авторов, например, работы Maise G., McDonald H. (“AIAA J.”, 1968, V. 6, No.1), где сравниваются данные при  и . Найдем теперь распределение плотности газа в пограничном слое при сверхзвуковом течении. При этом используем уравнение газового состояния (4.25), в котором – термодинамическая температура. Выразим ее через температуру торможения . Для этого воспользуемся подобием профилей скоростей и температур. При сверхзвуковом течении подобие имеет место между скоростями и температурами торможения: