Асимптотическая теория турбулентного пограничного слоя, страница 6

 –  скорость,

  –  плотность,

  –  вязкость,

 –  удельная теплоемкость при постоянном давлении,

  –  число Прандтля;

·   параметры вторичного потока:

  – массовый поток охладителя, или

 –  температура стенки

   –   энтальпия охладителя,

  –   удельная теплоемкость охладителя;

·   для осесимметричного потока;

– диаметр.

Параметры, которые должны быть вычислены:

 – температура стенки,

 –  массовый поток охладителя, а также другие производные характеристики:

  – число Стентона,

 – плотность теплового потока на стенке,

  – коэффициент трения,

 – касательное напряжение,

 – сила сопротивления,

   –  концентрация охладителя на стенке.

1. Известен массовый поток охладителя на стенке .

Запишем интегральное уравнение энергии в общем случае для осесимметричного течения

,         (4.82)

где ,    ,

,   , ,  ,

,     .

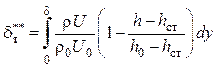Подставляя выражения для  и  в (4.82) и интегрируя от  до , получаем число Рейнольдса :

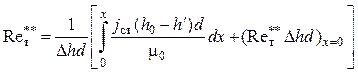,           (4.83)

где  зависит от предыстории потока и получается из расчета  поверхности, расположенной перед пористой пластиной.

Поскольку  – неизвестная величина, мы ее находим методом итерации, принимая за нулевое приближение .

Число Стентона в «стандартных» условиях

 ,                                 (4.84)

для  , :   ,  .

Параметр вдува

.                                        (4.85)

Энтальпийный фактор

.                                              (4.86)

Критический параметр вдува при    

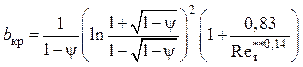;                     (4.87)

при

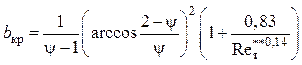    ,                   (4.88)

где 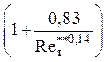 –  учитывает влияние конечности числа Рейнольдса на критический параметр вдува.

Предельная относительная функция теплообмена, учитывающая влияние неизотермичности на теплоообмен:

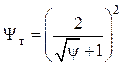.                                      (4.89)

Предельная относительная функция теплообмена, учитывающая влияние вдува на теплоообмен

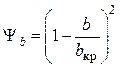.                                      (4.90)

Совместное влияние неизотермичности и вдува

.

Число Стентона

.                                    (4.91)

Из определения числа Стентона

находим новое приближение для

 .                         (4.92)

После подстановки нового значения  из (4.92) в (4.83) делаем следующее приближение по формулам (4.82)–(4.92) и так далее, до тех пор, пока относительная разность между текущим и предшествующим значениями  не станет меньше наперед заданной малой величины.

Далее определяем искомую величину 

,

теплоемкость смеси газов на стенке

.

Для бинарной смеси

.

Тепловой поток на стенке

.

Концентрацию вдуваемого охладителя на стенке в текущем сечении получаем из подобия процессов тепломассообмена

 .

                                   .

Коэффициент трения

                                     .

Касательное напряжение

                                     .

Сила сопротивления на единицу ширины обтекаемой поверхности

                                     .

2. Известна температура стенки 

Вычисляем энтальпию смеси газов на стенке

.              (4.93)

Поскольку  неизвестна, определяем ее методом итераций. За нулевое приближение принимаем .

Определяем параметр К:

.

Энтальпийный фактор

                                      .

Влияние неизотермичности на теплообмен

.

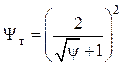Критический параметр вдува:

при                 

;

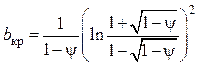при                 

 .

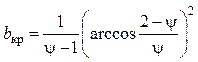Параметр проницаемости

.

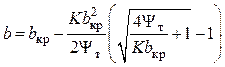Функция, учитывающая влияние вдува,

.

Из решения интегрального уравнения энергии

,

.

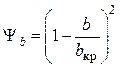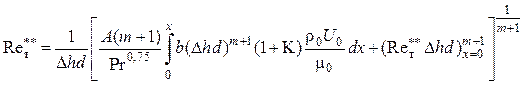Число Стентона в стандартных условиях

.

Число Стентона в реальных условиях

.

Массовый поток охладителя через стенку

.

Из подобия тепломассообмена

.

Полученное значение  подставляем в (4.93) и выполняем новое приближение, и так до тех пор, пока предыдущее и последующее значения не будут отличаться на малую наперед заданную величину.

Тепловой поток

.

Коэффициент трения

.

Касательное напряжение на стенке

.

Сила сопротивления на длине от  до  на единицу ширины канала

.