Асимптотическая теория турбулентного пограничного слоя, страница 3

,                                           (4.30)

где  и  – температуры торможения газа основного потока в рассматриваемой точке пограничного слоя и на стенке при обтекании адиабатической поверхности. Эти температуры находятся с учетом коэффициента восстановления  температуры на стенке :

.                                         (4.31)

Преобразуем второй член в уравнении (4.31)

,

где  – скорость звука.

Поскольку  ,  ,   – число Маха, имеем

.

С учетом значения газовой постоянной  , получаем

.

Тогда уравнение (4.31) имеет вид

.

Отсюда термодинамическая температура

 .                              (4.32)

Подставляя в (4.32) значение  из (4.30), имеем

.                  (4.33)

Делим (4.33) на :

.

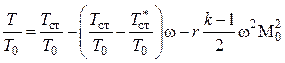Обозначим   ,     ,    , тогда 

.                             (4.34)

Так как , то  и уравнение (4.34) будет иметь вид

.                              (4.35)

Параметр  называется фактором теплообмена. Как только температура обтекаемой поверхности  отклоняется от адиабатической температуры  , между поверхностью и потоком начинается процесс теплообмена.

Если – тепловой поток направлен к поверхности, если  –  поверхность отдает тепло потоку.

Подставляя (4.34) в (4.25) и (4.23), имеем

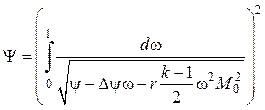.                      (4.36)

Уравнение (4.36) представляет собой табличный интеграл типа

и может быть проинтегрировано.

В результате интегрирования получаем относительный закон трения и теплообмена, учитывающий влияние сжимаемости и неизо-термичности

–

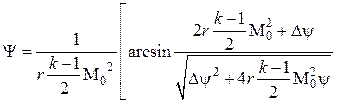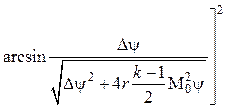–.                       (4.37)

Зависимость  от  и  демонстрируется графиком рис. 4.2.

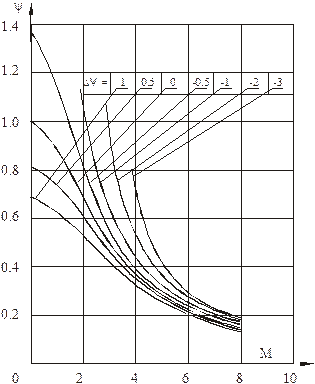
Рис. 4.2. Влияние сжимаемости на теплообмен

Для адиабатического течения  и уравнение (4.37) имеет вид

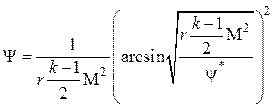.                  (4.38)

Учитывая преобразование тригонометрической функции

,                               (4.39)

уравнение (4.38) можно записать

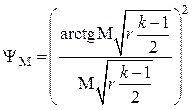.                              (4.40)

Расчет по этой формуле приведен на рис. 4.2 как расчет для .

Сполдинг предложил относительно простую аппроксимацию уравнения (4.37), которая с точностью до нескольких процентов справедлива до чисел Маха ~6 и имеет вид

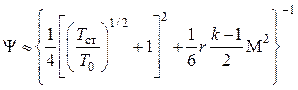.                  (4.41)

Принимая  и , получаем

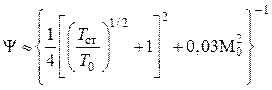.                      (4.42)

Для условий теплообмена на поверхности, обтекаемой сверхзвуковым потоком (совместное влияние неизотермичности и сжимаемости), хорошие результаты  дает аппроксимация:

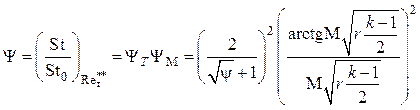.       (4.43)

Несмотря на то, что (4.43) получено для области , оно удовлетворительно описывает опытные данные и в области конечных значений чисел Рейнольдса и может быть рекомендовано для практических расчетов (рис. 4.3).

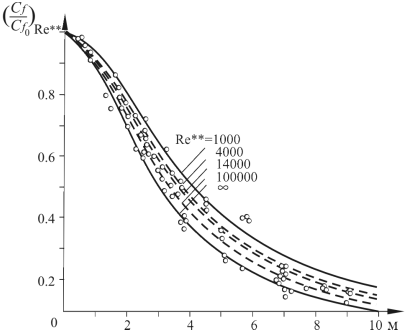
Рис. 4.3. Влияние сжимаемости на трение при разных

числах Рейнольдса

4.3.  Обтекание проницаемой стенки

Расчет турбулентного пограничного слоя на проницаемой стенке имеет чрезвычайно важное значение. Процессы такого рода возникают при защите элементов машин от воздействия потоков газа с высокой температурой («пористое» охлаждение лопаток газовых турбин, камер сгорания ракетных двигателей и т.п.), при испарении и конденсации, при наличии химических реакций на поверхности теплообмена, при затвердевании жидкости и плавлении твердых тел.

Рассматриваемая схема турбулентного пограничного слоя на проницаемой пластине показана на рис. 1.6.

Аппроксимация профиля тепловых потоков

(касательных напряжений)

Как было показано, основной предельный интеграл Кутателадзе–Леонтьева имеет вид

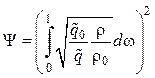                      .                                 (4.44)

Видно, что в случае обтекания проницаемой поверхности для решения интеграла (4.44) необходимо знать распределение плотности теплового потока в пограничном слое .

Получим аппроксимацию распределения плотности тепловых потоков. Из определения теплового пограничного слоя конечной толщины имеем условия:

при       ,                                                       (4.45)

при                  .

Из условия плавности функции  в точке   следует, что