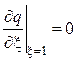Асимптотическая теория турбулентного пограничного слоя, страница 4

.                                           (4.46)

Уравнение энергии для пограничного слоя имеет вид

.                                (4.47)

Вблизи стенки  уравнение (4.47) будет

,

или

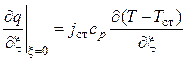,     .              (4.48)

Этим условиям удовлетворяет кубическая парабола

 .                                (4.49)

Определим постоянные коэффициенты :

                                      ,                             (4.50)

                                   ,                     (4.51)

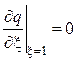,   ,    ,       (4.52)

,       ,

,

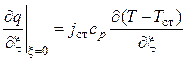.                                   (4.53)

Из (4.52):  , из (4.51): ,

.

,                    (4.54)

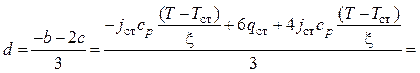
                            (4.55)

Найдем распределение : подставим в (4.49) коэффициенты из (4.50), (4.53), (4.54), (4.55), сделаем математические преобразования, в результате получим:

.

Из подобия   выразим  , подставим в предыдущее уравнение, умножим и разделим на , получим

,                           (4.56)

где  

,       .                  (4.57)

Из уравнения (4.56) видно, что распределение плотности теплового потока в пограничном слое не зависит ни от неизотермичности (), ни от сжимаемости (число М). Поэтому для таких течений мы брали  .

На непроницаемой поверхности :

.                                     (4.58)

Отношение тепловых потоков будет:

,

где 

.                                    (4.59)

Для условий  наиболее существенной для   (и  становится пристенная область, где  . Следовательно, можно принять

.                                       (4.60)

Распределение теплового потока по сечению пограничного слоя на проницаемой и непроницаемой стенках показано на рис. 3.10.

Распределение теплового потока в пограничном слое с вдувом газа показано на рис. 4.4.

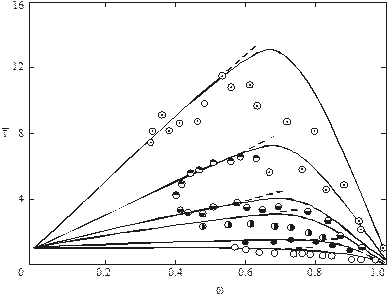
Рис. 4.4. Влияние вдува газа на распределение теплового потока

по сечению пограничного слоя. Кривые-расчет по (4.60)

для b₁ = 0…20

Предельный относительный закон тепломассообмена

на проницаемой стенке в условиях неизотермичности

Подставив распределение плотности теплового потока (4.60) в основной интеграл (4.44), получим выражение

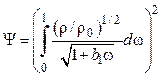                                (4.61)

или

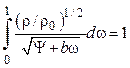,                                     (4.62)

где .

Относительная плотность  всегда конечна, а относительная скорость  изменяется от 0 до 1, и, следовательно, существует некоторое значение параметра проницаемости , при котором интегралу (4.62) соответствует . Такую величину параметра проницаемости будем называть критической и обозначать через . Это явление можно отождествлять с оттеснением пограничного слоя от проницаемой поверхности.

Критический параметр проницаемости определяем из уравнения (4.62), полагая :

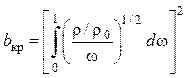 .                               (4.63)

Вдуваемый через стенку газ в общем случае может отличаться по своим свойствам от газа основного потока. Поэтому будем различать вдув однородного () и неоднородного газа ().

Для простейшего случая вдува однородного газа в изотермических условиях  из уравнений (4.62) и (4.63) имеем

,                                         (4.64)

.                                         (4.65)

Поскольку  при , уравнение (4.64) в общем случае записывают как

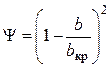.                                       (4.66)

Предельные относительные законы теплообмена и трения для случая вдува однородного газа в дозвуковой поток газа в неизотермических условиях получаются после подстановки выражения для плотности

                                  (4.67)

в основной интеграл (4.61):

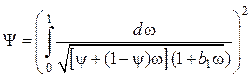.                      (4.68)

Интегрирование (4.68) дает следующие выражения для относительной функции теплообмена:

а) при

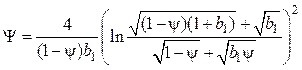;                 (4.69)

б) при

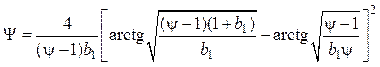.      (4.70)

Для критических параметров вдува из уравнения (4.63) с учетом (4.67) получаем:

а) при

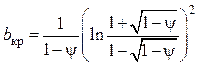;                           (4.71)

б) при 

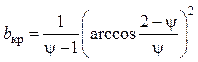 .                          (4.72)

Достаточно хорошей аппроксимацией уравнений (4.69) и (4.70) является уравнение