Пусть статическая характеристика преобразования y=f(x) с высокой точностью, существенно превышающей требуемую точность определения этой характеристики, аппроксимируется степенным полиномом неизвестной степени q с неизвестными коэффициентами:
 у = а0
+a1x + a2x2+...+aqxq. (3.32)
у = а0
+a1x + a2x2+...+aqxq. (3.32)
|
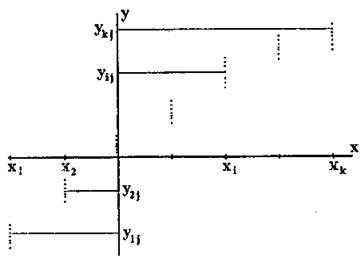
Рис. 3.3. Графическое представление результатов экспериментов по определению статической характеристики преобразования |
Обычно в нормативных документах на испытуемое средство измерений указываются значения х1,х2,...,хк, которые должны быть заданы на входе. С помощью калибратора или иного точного источника входной величины х устанавливают последовательно указанные значения, начиная с наименьшего, и при каждом значении хi=1,2,..., к измеряют выходной сигнал. Затем по достижении последнего к-го значения и измерения выходного сигнала ненамного увеличивают значение входной величины, и процесс повторяется в обратном направлении. Делают несколько таких циклов в одинаковых условиях. В результате при каждом значении входной величины хj будет получен массив выборочных значений выходной величины объёмом n: yi1, yi2,… yin Пример графического представления результатов описанного эксперимента показан на рис. 3.3. Здесь yij= i=l,2,...,k; j = 1,2,...,n - обозначение выборочных значений выходной величины, полученных в i -ой точке при j -ом эксперименте.
3.5.2. Предварительная обработка результатов измерений
Предварительная обработка данных, полученных в результате эксперимента и представленных на рис. 3.3, заключается в том, что в каждой i -ой точке вычисляются оценки математического ожидания и дисперсии (см. также п.3.2.1):
![]() (3.33)
(3.33)
Вслед за этим проверяется статистическая гипотеза о равенстве дисперсий разброса результатов измерений в i -ых точках. На языке математической статистики эта гипотеза формулируется вместе с ее альтернативой следующим образом:
Гипотеза
H0:![]() - "измерения
равноточные".
- "измерения
равноточные".
Альтернатива Н1: - "измерения неравноточные".
Проверка этой гипотезы необходима для выбора одного из двух различающихся методов обработки данных. Общие принципы проверки статистических гипотез изложены выше в п.3.4.
Проверка сформулированной гипотезы выполняется по критерию Кочрена (Cochran). Для этого вычисляется значение критерия
![]() (3.34)
(3.34)
Вычисленное значение критерия сравнивается с критическим значением, которое зависит от k и n, а также от уровня значимости α, значение которого выбирается из диапазона 0.05 - 0.2. В таблице 3.5 приведены критические значения g(α,k,n) для α=0.05.
Если окажется, что G > g(α,k,n) то это значит, что мы не имеем достаточных оснований для того, чтобы считать нашу гипотезу справедливой, а измерения выходной величины следует считать неравноточными. В противном случае у нас нет достаточных оснований для отклонения гипотезы Н0, и мы считаем измерения равноточными.
Вероятность ошибочного отклонения нулевой гипотезы, если она на самом деле справедлива, будет не больше заданной нами вероятности α.
Таблица 3.5
Критические значения критерия Кочрена
|
n\k |
2 |
3 |
4 |
5 |
6 |
7 |
|
6 8 10 12 |
0.8772 0.8332 0.8010 0.7910 |
0.7071 0.6530 0.6167 0.5020 |
0.5895 0.5365 0.5017 0.4780 |
0.5063 0.4564 0.4241 0.4020 |
0.4447 0.3980 0.3682 0.3460 |
0.3974 0.3535 0.3259 0.3050 |
Результаты выполненной нами предварительной обработки исходных данных запишем в виде вектора средних значений и матрицы оценок дисперсий:
|
|
(3.35)
3.5.3. Определение статической характеристики преобразования. Случай равноточных измерений
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.