Другие предметы \ Метрология, стандартизация, сертификация и техническое документирование

Методы математической статистики, применяемые в практике измерений. Подготовка массива результатов измерений для статистической обработки. Вариационный ряд, страница 15

В противоположной ситуации, когда   делается заключение: "Выборочные данные не противоречат гипотезе о том, что они извлечены из генеральной совокупности с плотностью распределения φ(х)".

3.6.3. Проверка гипотезы Н0 о соответствии плотности распределения выборочным данным по критерию Колмогорова - Смирнова

В соответствии с настоящим критерием сопоставляются функции распределения: предполагаемая и выборочная (см. п. 3.1.2). В качестве меры расхождения между ними здесь используется максимальный модуль разности:

                           (3.60)

где F(x(i)) - предполагаемая функция распределения.

Заданному уровню значимости соответствует критическое значение критерия Da, и если окажется, что D > Da, делается заключение: "Если бы полученная нами выборка была извлечена из генеральной совокупности с плотностью распределения φ(х), то такое большое значение критерия настолько маловероятно, что у нас нет оснований для подтверждения выдвинутой гипотезы".

В противоположной ситуации, когда D < Da, делается заключение: "Выборочные данные не противоречат гипотезе о том, что они извлечены из генеральной совокупности с плотностью распределения φ(х)".

Таблица 3.9

Критические значения Da

 

a\N

10

15

20

25

30

35

40

50

60

80

100

0.2

0.322

0.266

0.231

0.208

0.190

0.176

0.165

0.148

0.136

0.118

0.106

0.1

0.369

0.304

0.265

0.238

0.217

0.202

0.189

0.169

0.155

0.135

0.121

0.05

0.409

0.337

0.294

0.264

0.242

0.224

0.210

0.118

0.172

0.150

0.134

Для корректного применения критерия. Колмогорова-Смирнова нужно разделить выборку на две группы, по одной из них оценить параметры предполагаемой функции распределения, а по другой - построить выборочную функцию распределения и приступать к проверке гипотезы.

В таблице 3.9 приведена выписка из таблицы критических значений Da/

3.6.4. Проверка гипотезы Н0 о соответствии плотности распределения выборочным данным по критерию ω2 Мизеса

Мерой расхождения между предполагаемой и выборочной функциями распределения является средний квадрат разностей между ними:

     (3.61)

Это выражение существенно упрощается, если интеграл представить в виде суммы интегралов по интервалам (хi,хi+1). Тогда после умножения на nбудем иметь:

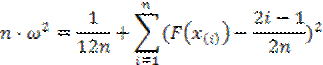
где i- номер члена вариационного ряда, F(x(i)) - предполагаемая функция распределения.

Точные критические значения а не табулированы, но уже начиная с объема выборки n=50, можно уверенно пользоваться значениями, которые приведены в нижеследующей таблице.

Таблица 3.10

Критические значения критерия Мизеса

Уровни значимости

0.2

0.1

0.05

0.03

Критические значения   n а

0.2415

0.3473

0.4614

0.5489

Теперь если окажется, что n>n делается заключение: "Если бы полученная выборка была извлечена из генеральной совокупности с плотностью распределения φ(х), то такое большое значение критерия настолько маловероятно, что у нас нет оснований для подтверждения выдвинутой гипотезы".

В противоположной ситуации, когда n<n, делается заключение: "Выборочные данные не противоречат гипотезе о том, что они извлечены из генеральной совокупности с плотностью распределения φ(х)”

Скачать файл