Методы математической статистики, применяемые в практике измерений. Подготовка массива результатов измерений для статистической обработки. Вариационный ряд, страница 13

              (3.48)

После этого с использованием таблиц 3.6, 3.7 проверяется выполнение неравенства (3.42). Если неравенство (3.42) выполняется, это значит, что фактическая нелинейность, если она есть, настолько мала, что не может быть выявлена на фоне погрешностей измерений. В противном случае нелинейность обнаруживается, и пользователь принимает одно из двух решений:

- повышать степень аппроксимирующего полинома и тем самым уточнять характеристику преобразования данного конкретного экземпляра средства измерений,

- учесть обнаруженную нелинейность в составе погрешности средства измерений.

Однако, следует иметь в виду, что гипотеза о линейности может быть отклонена не только из-за фактической нелинейности характеристики преобразования. Ее отклонение может быть вызвано некорректностью выполнения эксперимента (см. также замечание к п. 3.5.3.).

В конечном итоге мы получаем оценку статической характеристики преобразования средства измерений в виде

у=₁-х.                     (3.49)

Случай неравноточных измерений.

Если проверка статистической гипотезы о равенстве дисперсий измерений выходной величины дала отрицательный результат, то формулы (3.47) изменяются следующим образом:

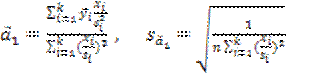      (3.50)

Остальные действия, проверка гипотез, выводы и замечания в точности соответствуют изложенному выше.

3.5.6. Оценка характеристик погрешности средства измерений по результатам определения линейной статической характеристики преобразования

Поскольку в эксперименте по определению характеристик погрешности средств измерений применяются образцовые средства высокой точности, можно считать, что все экспериментальные значения погрешности суть выборочные значения погрешности испытуемого средства измерений.

После того, как оценка статической характеристики преобразования испытуемого средства измерений получена в виде (3.49), мы имеем возможность вычислить выборочные значения погрешностей в каждой i-ой точке диапазона измерений :

                                              (3.51)

Таким образом в каждой i- ой точке мы получаем выборку объема n (см. рис. 3.4):

                                               (3.52)

Для каждой из этих выборок по формулам (3.17) вычисляются оценки систематической составляющей погрешности и среднеквадратического значения случайной составляющей погрешности:

      (3.53)

Далее в соответствии с п. 3.3.4.1. для заданных значений вероятностей Р и Q вычисляются параметрически толерантные пределы в каждой i - ой точке :

 ]  (3.54)

и по ним в соответствии с п. 2.4 и формулой (3.26) определяют оценки  полуширины интервалов Jpi, содержащих не менее Р -ой доли всех возможных значений аддитивной погрешности средства измерений в i -ой точке диапазона измерений:

             (3.55)

В качестве оценки характеристики аддитивной погрешности следует принять наибольшее значение по всем i, i = 1,2,...,k:

                 (3.56)

Такое определение характеристики аддитивной погрешности позволяет считать, что если статическая характеристика преобразования средства измерений обладает некоторой нелинейностью, то систематическая погрешность, вызванная этой нелинейностью, учитывается в составе характеристики погрешности (3.56).

Пример графического представления значений погрешности  (точки), их средних арифметических  (звездочки), оценок (, границ интервалов J_Pi(отрезки горизонтальных линий), и границ (-,+) аддитивной погрешности (горизонтальные прямые) представлен на рис. 3.4

 

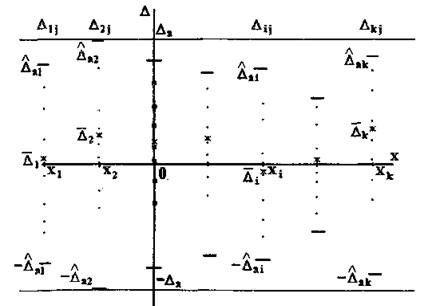Рис.3.4. Графическое представление выборочных значений погрешности средства измерений и границ симметричных относительно нуля параметрических толерантных пределов погрешности