Методы математической статистики, применяемые в практике измерений. Подготовка массива результатов измерений для статистической обработки. Вариационный ряд, страница 5

- коэффициент Стьюдента, таблицы значений которого приводятся практически во всех учебниках и справочниках по математической статистике; ниже в таблице 3.1 приведена выписка из этих таблиц.

Таким образом, по определению доверительного интервала,

      (3.21)

В случае отсутствия систематической составляющей погрешности доверительный интервал с границами (3.20) есть не что иное, как интервал неопределенности истинного значения измеряемой величины (см. также п.2.1). Как видно из формулы (3.21), с увеличением n ширина доверительного интервала уменьшается, стремясь в пределе к нулю. Это обстоятельство свидетельствует о том, что увеличение количества измерений и усреднение результатов небесполезно. Систематическую погрешность усреднение результатов измерений не изменяет.

Границы доверительного интервала для систематической составляющей погрешности средства измерений определяются при его метрологических испытаниях по выборочным значениям погрешности в соответствии с приведенными формулами и с заменой х на Δ. В результате будут получены нижняя Δ_си „ и верхняя Δ_св, границы доверительного интервала, который с вероятностью Q накрывает действительное значение систематической составляющей погрешности средства измерений:

      (3.22)

где точечные оценки  и s вычисляются по формулам (3.17).

Таблица 3.1

Коэффициенты Стьюдента 

В п. 2.6 приводится пример интервальной оценки характеристики погрешности среднего арифметического значения, полученного усреднением результатов многократных измерений (пример 2).

3.3.3. Доверительные интервалы для среднеквадратического значения случайной составляющей погрешности

Все действия и формулы, необходимые для построения доверительных интервалов, накрывающих действительное среднеквадратическое значение а случайной составляющей погрешности средств измерений и результатов измерений, полностью идентичны. Различие состоит только в обозначениях.

Вычисление границ доверительного интервала для а основано на том, что если плотность распределения случайной составляющей погрешности нормальна, то плотность распределения величины

         (3.23)

где s - оценка σ по формуле (3.7) или (3.17), есть плотность распределения Х²(n- 1) с (n-1) степенью свободы. Поэтому

откуда, преобразуя неравенство, стоящее внутри скобок, получим нижнюю σ_н и верхнюю σ_в границы доверительного интервала, накрывающего действительное значение σ с доверительной вероятностью Q :

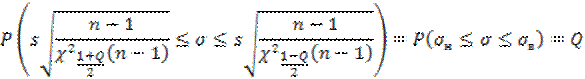
Поскольку σ≥ 0, нас будет интересовать только верхняя граница доверительного интервала σ_в. Значение этой верхней границы для σ определяется из неравенства, стоящего в круглых скобках предыдущего выражения

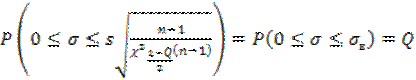          (3.24)

Таблицы квантилей распределения χ²(n-1) приведены практически во всех учебниках и справочниках по математической статистике. Ниже в таблице 3.2 приведена выписка из этих таблиц применительно к представленному здесь циклу лабораторных работ.

Таблица 3.2

Значения   χ2_1-Q(n-1)