Другие предметы \ Метрология, стандартизация, сертификация и техническое документирование

Методы математической статистики, применяемые в практике измерений. Подготовка массива результатов измерений для статистической обработки. Вариационный ряд, страница 10

Поскольку степень полинома q неизвестна, мы вынуждены отыскивать полином, аппроксимирующий статическую характеристику преобразования с подбором подходящей степени. Пусть предполагаемая степень искомого полинома равна р. Тогда мы хотели бы, чтобы во всех i - ых точках выполнялись равенства:

      (3.36)

Эти равенства образуют систему уравнений, которая может быть записана в матричном виде

,          (3.37)

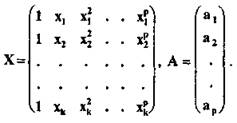
где вектор Y определен в (3.35). Матрица X и вектор А имеют вид

 


Всегда желательно, чтобы к > р + 1. Таким образом создается полезная избыточность, повышающая устойчивость оценок коэффициентов полинома. Но при этом матрица X неквадратная, и система (3.37) не имеет решения в обычном смысле. Для получения решения эту систему преобразуют к системе с •квадратной матрицей путем умножения слева на транспонированную матрицу XT

XT = XTXA,

Решая эту систему, получают вектор оценок коэффициентов полинома:

 = (XTX)-1XT.                  (3.39)

Компонентами вектора  являются оценки коэффициентов полинома (3.36). Описанный метод их получения называется методом наименьших квадратов (МНК).

Для того, чтобы оценить дисперсии погрешности оценок коэффициентов, следует найти наибольшую из оценок дисперсии , полученных по (3.33), и вычислить дисперсионную матрицу оценок коэффициентов:

                         (3.40)

Диагональные элементы этой матрицы суть дисперсии искомых коэффициентов. Появление множителя 1/n вызвано тем, что левая часть системы (3.37) - это вектор средних арифметических значений, дисперсия которых, как указано в п. 3.2.1, в n раз меньше дисперсии погрешности однократных измерений.

Формулируется статистическая гипотеза

Н0: "степень полинома не превышает р"

вместе с сопровождающей ее альтернативой

Н1,: "степень полинома превышает р".

Для проверки этой гипотезы полученные оценки коэффициентов подставляются в полином (3.36), (3.37), во всех i -ых точках вычисляются отклонения значений этого полинома от средних значений  и находится сумма квадратов этих отклонений, взвешенных обратно пропорционально оценкам дисперсий погрешностей измерений в этих точках:

       (3.41)

где S-1 - матрица, обратная матрице, определенной в (3.35).

Сформулированная гипотеза проверяется с помощью упрошенного критерия Фишера и сводится к проверке неравенства

         (3.42)

где а - уровень значимости (см. п. 3.4). Значения  приведены в таблицах 3.6, 3.7 для уровней значимости 0.05 и 0.1 . В этих таблицах обозначено :

k1=k-p-l,k2=n-l.

Если неравенство (3.42) выполняется, делается вывод о том что наша гипотеза не противоречит экспериментальным данным. В противном случае приходится сделать вывод, что выбранная нами степень полинома недостаточна, то есть р<q.

Таблица 3.6

Критические значения критерия Фишера, а=0.05

k2\ k1

3

4

5

6

7

8

9

10

11

12

5

5.41

5.19

5.05

4.95

4.88

4.82

4.77

4.73

4.68

4.62

7

4.35

4.12

3.97

3.87

3.79

3.72

3.68

3.63

3.57

3.51

9

3.86

3.63

3.48

3.37

3.29

3.23

3.18

3.14

3.07

3.00

11

3.58

3.36

3.20

3.09

3.01

2.95

2,90

2.85

2.79

2.72

13

3.41

3.18

3.02

2.91

2.83

2.77

2,71

2.67

2.63

2.60

15

3.29

3.05

2.90

2.79

2.71

2.64

2.59

2.54

2.50

2.47

17

3.19

2.96

2.81

2.70

2.61

2.55

2.49

2.45

2.41

2.38
Скачать файл