Виды параллельных проекций. Изображение плоских фигур в свободной параллельной проекции. Теорема Польке-Шварца

Методы

Изображений

Методические рекомендации и задания

для контрольных работ студентов

 математического факультета

Составитель:

Тара 1999

Содержание

§1.  Введение. Виды параллельных проекций.....................................................1

§2. Изображение плоских фигур в свободной параллельной проекции..........................................................................................................2

§3. Теорема Польке-Шварца................................................................................7

§4. Изображение сферы и фигур, вписанных в сферу и описанных около нее........................................................................................................8

§5. Решение простейших позиционных задач...................................................10 

§6.  Построение плоских сечений многогранников..........................................13

§7. Аксонометрические проекции. Частные случаи аксонометрии.................14

§8. Метрически определенные изображения...................................................19

§9. Требования к оформлению контрольной работы......................................22

§10. Формулировка заданий контрольной работы..........................................24

Приложения......................................................................................................26

Литература……………………………………………………………………….32

§ 1. Введение. Виды параллельных проекций.

Когда говорят «изображение», то представляют себе плоскую фигуру (образ на доске, бумаге и т.д.), по которой можно узнать оригинал (предметы окружающей среды).

При выполнении изображений опираются на методы изображений - совокупность правил черчения, определяющих порядок действий при построении изображения плоского или пространственного предмета; при этом полагаем, что изображение должно быть:

1)  верным (отражать свойства фигуры),

2)  наглядным (давать ясное представление о предмете),

3)  легко выполнимым (мелом на доске, карандашом в тетради во время урока).

Приведенным требованиям достаточно полно удовлетворяют параллельные проекции.

     Если в пространстве задана плоскость a и точка A’ (A’Ïa). Спроектируем точку A’ на плоскость a в некотором направлении  l ||  a (рис. 1):

AA’Ça=A, где AA’|| l.

Точка A называется параллельной проекцией точки A’ на плоскость a.

Параллельные проекции обладают следующими свойствами:

1)  проекцией точки является точка;

2)  прямая преобразуется в прямую;

3)  если точка принадлежит линии (прямой или кривой), то проекция точки принадлежит проекции этой линии;

4)  для любых точек A’,B’,C’ одной прямой и их образов A,B,C сохраняется простое отношение трех точек прямой, обозначаемое  (А’В’С’)=(АВС) (т.е. если точка С’ делила отрезок А’В’ в некотором отношении, то ее образ - точка С будет делить AB - проекцию отрезка в том же отношении, причем C’ может лежать как внутри, так и вне A’B’, ) (рис. 1);

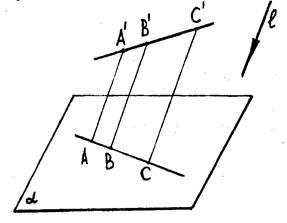
Рис. 1

5)  проекции параллельных прямых параллельны.

Различают ортогональное (прямо-угольное) и косоугольное параллельное проектирование (рис. 2): К₁ - ортогональная проекция, К₂ - косоугольная.

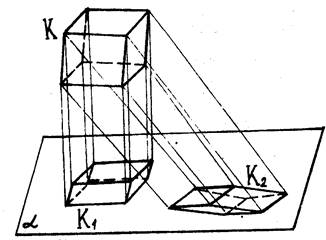
Рис. 2

При ортогональном проектировании направление проектирования l перпендикулярно плоскости проекций a, при косоугольном l составляет с a произвольный острый угол.

Однако, стоит заметить, что, например, изображение сферы будет наглядным только при ортогональном проектировании, т.к. прямоугольная проекция сферы - это всегда круг, а косоугольная - эллипс.

Построение изображений на доске и в тетради во время урока является произвольным, т.е. находится одно из возможных изображений, которое сохраняет свойства проектируемой фигуры, но не требует уточнения направления проектирования и расположения оригинала относительно плоскости проекций. Такое параллельное проектирование называют свободным.

 Определение. Свободная параллельная проекция - это верное и по возможности наглядное изображение фигуры, которое могло бы быть получено при каком-нибудь параллельном проектировании.

Далее будем рассматривать вопрос: как выглядят всевозможные параллельные проекции заданных фигур?    

§2. Изображение плоских фигур в свободной параллельной  проекции.

Свойство 1. Любой наперед заданный эллипс может служить ортогональной проекцией некоторой окружности.

Доказательство:

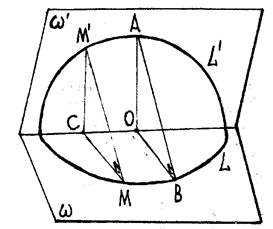
Рис.3

Спроектируем окружность L’Îw¢ в некоторую линию LÎw (рис. 3), тогда радиус АО окружности спроектируется в отрезок ВО. Если угол наклона плоскости w¢ к плоскости w равен j, то cosj =, при этом всякая полухорда CM’, параллельная радиусу AO, спроектируется в отрезок CM, где CM || BO, причем выполняется условие:

CM/CM’=cosj,                              (*)

т.е. между соответствующими хордами оригинала (окружность L’) и изображения (линия L) имеем пропорцию (*) с коэффициентом k= cosj. Значит, линия L - эллипс, т.к. именно эллипс получается сжатием окружности в k раз.

Выбрав радиус окружности равным полуоси эллипса и изменяя угол j, будем получать эллипсы различной формы, среди которых найдется заданный эллипс.

Следствие 1. Сопряженные диаметры1) окружности проектируются в сопряженные диаметры эллипса.