, v=w=1,
а угол между аксонометрическими осями O1y1 и O1x1 равен
углу между O1x1 и O1z1 и равен 135о (рис. 24).
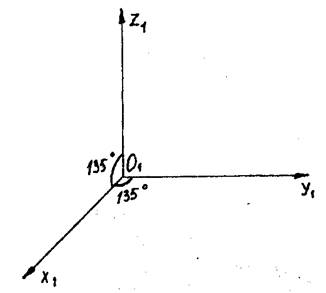
Рис.24
Пример 1. Во фронтальной кабинетной проекции изобразить куб, если его расположение по отношению к реперу показано на виде сверху (рис. 25, а).
Решение. Изображаем основание куба во фронтальной кабинетной проекции,
для которой, v=w=1,
т.е. все отрезки, принадлежащие оси Oy или ей параллельные, строятся
в натуральную величину (в том числе O1Dy1, O1B1, O1Cy1 и т.д.
(рис. 25, б). Исходя из этих данных, изображаем основание куба. Далее получаем
изображение куба, считая, что его боковые ребра параллельны плоскости yOz и
изображаются в натуральную величину.
Замечание. К достоинствам кабинетной проекции относят легкость исполнения, а к недостаткам - свойство, связанное с косоугольностью (например, изображение сферы, вписанной в куб, не будет наглядным).
II. Прямоугольная аксонометрия.
Теорема. Для прямоугольной аксонометрии сумма квадратов показателей искажений равна двум, т.е. u2+v2+w2=2.
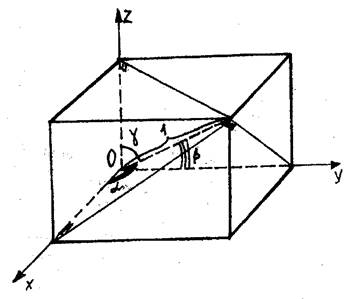
Рис.26
Доказательство. Сначала покажем, что в прямоугольном параллелепипеде с единичной диагональю, которая образует с координатными осями углы a, b, g, справедливо: cos2a+cos2b+cos2g=1. Действительно, пусть координатные оси направлены по трем измерениям параллелепипеда (рис. 26). Тогда единичная диагональ даст проекции на ось координат в виде x= cosa, y=cosb, z=cosg. Легко получить (используя теорему Пифагора)
cos2a+cos2b+cos2g=1. (1)
Теперь перейдем к непосредственному доказательству теоремы.
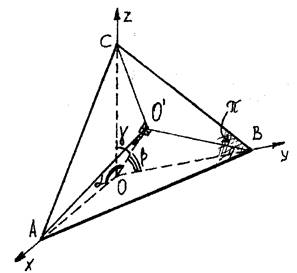
Рис.27
Пусть плоскость проекций p пересекает пространственный репер в точках A, B,C
(рис. 27), O’ - проекция точки O на плоскость p, O’A, O’B, O’C - проекции отрезков репера. OO’^ p и образует с
координатными осями углы a, b, g, тогда (по
доказанному выше) имеем: cos2a+cos2b+cos2g=1. Из DAOO’ получаем sina
, cos2a=1-sin2a=1-u2.
Аналогично cos2b=1-v2, cos2g=1-w2.
Подставим эти выражения в формулу (1), тогда 1- u2+1-v2+1-w2=1, т.е. u2+v2+w2=2.
Теорема доказана.
1) Прямоугольная изометрия: u = v = w.
Для того, чтобы в прямоугольном проектировании репера Oxyz на плоскость p получить равные показатели искажения, необходимо, чтобы углы между образами O1x1, O1y1, O1z1 были равны 120о. Кроме того, выражение u2+v2+w2=2 для изометрии примет вид 3u2=2, а значит,
u = v = w =
.
Замечание.
Иногда (для простоты) берут u = v = w = 1, что приводит к увеличению масштаба предмета в
1,22 (
)
раза.
Пример 2. Построить изображение правильной шестиугольной пирамиды, если известны ее высота h и сторона основания a.
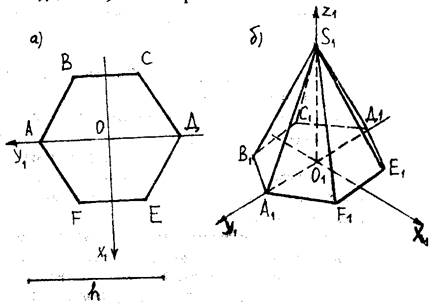
Рис.28
Решение. Изобразим оригинал основания пирамиды (рис. 28, а). Строим аксонометрическую систему координат O1x1y1z1 (рис. 28, б). Найдем точку А1 - проекцию точки А.
А1 принадлежит оси O1y1, т.к. ее прообраз находится на оси Oy. Кроме того, известно, что ОА=а, тогда О1А1=0,82а.
Аналогично, определяя положение вершин шестиугольника на оригинале, находим их положение в аксонометрических осях и соединяем в той же последовательности, что и на оригинале.
Далее ищем точку S1 - проекцию вершины пирамиды, из условий, что OS=h и точка S лежит на оси Oz.
2) Прямоугольная диметрия.
Диметрических проекций
может быть построено сколько угодно. Одна из них (наиболее удобная) имеет
соотношение коэффициентов 
, т.е.
v = w, 
.
Подставив эти данные в
формулу u2+v2+w2=2, получим
,
откуда 
,
тогда u = w = 0,94, v = 0,47.
Следовательно, в прямоугольной диметрической проекции по двум осям (или по прямым, параллельным этим осям) сокращение получается примерно 0,94, а по третьей - 0,47.
Для изображения выбирают оси:
O1z1 - вертикально,
O1y1 - под углом 7o10’ к горизонту,
O1x1 - под углом 41o25’ к горизонту.
Т.к. tg 7o10’
= 
, а tg 41o25’ = 
, то гипотенузы треугольников с данными соотношениями
катетов и будут указывать положение осей O1x1 и O1y1 (рис.
29).
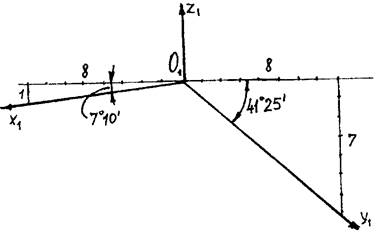
Рис.29
Замечание. Иногда берут v = w =
1, u = 
, тогда фигура выглядит увеличенной в 1,06 раза.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.