Виды параллельных проекций. Изображение плоских фигур в свободной параллельной проекции. Теорема Польке-Шварца, страница 3

Для доказательства достаточно достроить трапецию до параллелограмма.

В свободной параллельной проекции допустимо изображать:

- окружность любым эллипсом;

- треугольник любым треугольником;

- параллелограмм любым параллелограммом;

- четырехугольник любым четырехугольником с тем же отношением частей диагоналей;

- трапецию любой трапецией с тем же отношением оснований.

Приведем несколько примеров построения изображений правильных многоугольников, считая известными свойства каждого многоугольника.

     Пример 1. Построить изображение правильного пятиугольника в свободной параллельной проекции.

     Решение. Пусть A'B'C'D'E' - правильный пятиугольник (рис. 8, а). Проведем диагонали A'C' и B'D' и опишем около него окружность.

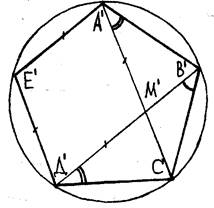
Рис.8,а

DD'B'C' ~ DB'M'C', т.к.

1.  ÐD'B'C' - общий,

2.  ÐB'C'A' =ÐB'D'C' - как вписанные углы, опирающиеся на равные дуги.

Тогда                                                     (**)

Т.к. A'E' || B'D', E'D' || A'C', A'E'=E'D' (из свойств правильного пятиугольника), то A'E'D'M' - ромб, т.е. M'D'=A'E'-B'C'.

Обозначим B'C'=a, B'M'=x.

Из равенства (**) имеем ,  ,  поэтому квадратное уравнение

l²+l-1=0 имеет корни, из которых один не удовлетворяет условию задачи, тогда, следовательно .

Отсюда получаем правило изображения правильного пятиугольника:

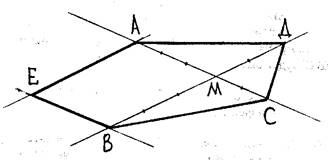
Рис.8,б

Проведем произвольную пару прямых, пересекающихся в точке М (рис. 8, б). На одной прямой отложим от  точки М три произвольных,  но равных отрезка по одну сторону и два таких же - по другую. Получаем точки B и D. Аналогичные построения для другой прямой (в общем случае откладываемые отрезки на второй прямой имеют другую длину) - точки А и С. Затем строим параллелограмм на отрезках BM и AM. Четвертая вершина параллелограмма - точка E.  ABCDE - изображение правильного пятиугольника.

     Пример 2. Построить изображение правильного шестиугольника.

Решение. Пусть A'B'C'D'E'F' - правильный шестиугольник (рис. 9, а).

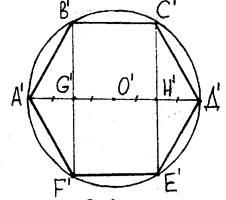
Рис.9,а

Опишем около него окружность и проведем отрезки A'D', B'F', C'E'. Тогда увидим, что диагональ A'D' разделилась точками G', H', O' (центр описанной окружности) на 4 равные части, причем B'C'||C'E'||F'E', A'B'||E'D', C'D'||A'F', B’F’||C’E’.               (1)

Тогда изобразить правильный шестиугольник можно следующим образом (рис. 9, б):

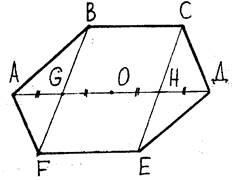
Рис.9,б произвольный отрезок AD делим на 4 равные части, получаем точки G, O, H. Учитывая условия (1), присущие оригиналу, достраиваем изображение ABCDEF.

Замечание 1.Существуют и другие способы построения правильного шестиугольника.  Например, зная, что B'C'E'F' - прямоугольник, изобразим его произвольным параллелограммом BCEF и достроим до шестиугольника, исходя из свойств оригинала A'B'C'D'E'F', которые сохранятся при параллельном проектировании.

Выявив некоторые признаки, присущие оригиналу - это могут быть как алгебраические равенства (пример 1), так и геометрические свойства (пример 2) - мы переносим их на изображение. Это относится и к построению изображений многоугольников, вписанных в окружность (или описанных около нее).

 Замечание 2.При построении фигур, вписанных или описанных около окружности, зная, что изображением окружности является эллипс, а взаимно перпендикулярные диаметры окружности перейдут в сопряженные диаметры эллипса, помещают вершины (одну или несколько) в концы сопряженных диаметров и рассматривают расположение многоугольника относительно сопряженных диаметров, а затем переносят эти свойства на изображение.

§3. Теорема Польке-Шварца.

Теорема Польке-Шварца. Любой плоский четырехугольник ABCD вместе с его диагоналями (сплошной и пунктирной) может служить параллельной проекцией тетраэдра A'B'C'D', если только не все вершины четырехугольника  лежат на одной прямой.

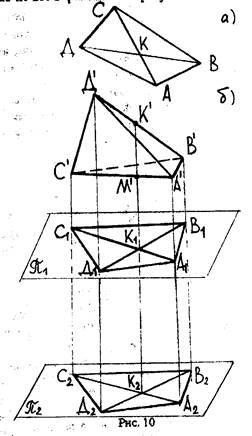
Доказательство. Пусть задан произвольный плоский четырехугольник ABCD (рис.10, а). Докажем, что он может служить параллельной проекцией тетраэдра A'B'C'D' (рис.10, б). Выберем на ребрах тетраэдра B’C’ и A’D’ точки K’ и M’ из условий: