Следствие 2. Касательная к эллипсу в конце одного из сопряженных диаметров параллельна другому из этих диаметров.
Исходя из свойства 1, рассмотрим способ построения точек эллипса, если даны его сопряженные диаметры.
Опишем около круга квадрат, стороны которого параллельны диаметрам A’B’ и C’D’ (рис. 4, а). Отметим произвольную точку M’, принадлежащую окружности: A’M’ÇC’D’=K’, C’F’ÇB’M’=L’.
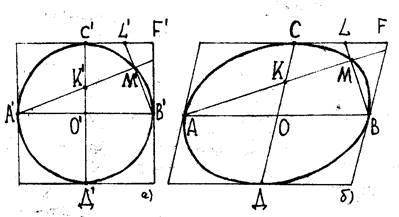
Рис.4
DA’O’K’=DL’B’F’ (A’O’=B’F’, ÐF’B’L’=ÐO’A’K’, ÐL’F’B’=ÐA’O’K’=90o).
Тогда
O’K’=F’L’, C’K’=C’L’, т.е. если попарно равны отрезки, то равны и их
отношения: 
, т.е.
отношение трех точек (C’K’O’) диаметра круга равно отношению трех точек (C’L’F’)
стороны описанного около него квадрата.
Диаметрам круга соответствует пара сопряженных диаметров эллипса: AB, CD (свойство 1, следствие 1). Квадрату, описанному около круга, будет соответствовать параллелограмм, описанный около эллипса, со сторонами, параллельными его диаметрам (свойство 1, следствие 2) (рис. 4, б). Если на отрезках C’O’ и C’F’ отметим точки K’ и L’, для которых (CLF)=(C’L’F’) и (CKO)=(C’K’O’), однако (CLF)=(CKO), тогда (C’K’O’)= (C’L’F’). Таким образом, точка K’ делит отрезок C’O’ в том же отношении, в каком L’ делит C’F’.
Предположим, что мы провели прямую B’L’ произвольно и
хотим построить на ней точку эллипса. Для этого достаточно найти K’ÎC’O’,
причем 
и
соединить ее с точкой A’. Тогда A’K’ÇB’L’=M’
(точка эллипса),
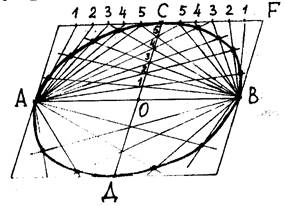
Рис.5
Само построение точек эллипса выполняется следующим образом. Пусть имеем сопряженные диаметры эллипса AB и CD (рис. 5). Делим отрезок CF на n равных частей и отрезок OC на такое же количество равных частей (причем части отрезков CF и OC в общем случае не равны), нумеруем точки деления: 1, 2, 3, ... . Для построения точек эллипса надо соединить точку A с точками 1, 2, 3, ... отрезка OC, а B - с точками 1, 2, 3, ... отрезка FC, тогда точки пересечения соответствующих прямых, например, A1 и B1, A2 и B2, ... , являются точками эллипса.
Свойство 2. Всякий параллелограмм может послужить ортогональной проекцией некоторого квадрата.
Свойство 3. Всякий треугольник с точностью до подобия может послужить ортогональной проекцией заданного произвольного треугольника.
Покажем, что DA'B'C' может давать ортогональную проекцию в виде треугольника, подобного DABC; опишем около DA'B'C' квадрат (рис. 6). Соотнесем D’ с треугольником, например, пересекая диагональю D’C’ сторону A’B’ в точке E’.
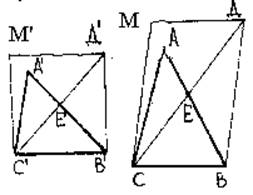
Рис.6
Поскольку при параллельной проекции сохраняется простое отношение трех точек, можно восстановить сначала точку E на стороне AB из условия (ABE)=(A’B’E’), (CED)=(C’E’D’). Затем восстанавливаем параллелограмм MDBC. Согласно свойству 2 существует ортогональная проекция квадрата в виде параллелограмма с формой ADFC. При этом и проекция A'B'C' будет иметь форму DABC.
Следствие. Если прямая треугольная призма имеет достаточно большую высоту, то среди ее плоских сечений можно отыскать треугольник любой наперед заданной формы.
Свойство 4.Если у двух четырехугольников A’B’C’D’ и ABCD диагонали в пересечении делятся в одинаковом отношении, то найдется способ расположить A’B’C’D’ в пространстве так, чтобы прямоугольная проекция имела форму ABCD.
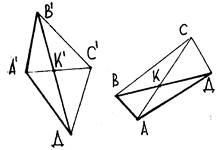
Рис.7
Доказательство. Выделим у четырехугольников треугольные фрагменты A’B’D’ и ABD (рис. 7). Согласно свойству 3 существует прямоугольная проекция A’B’D’, имеющая форму ABD. При этом образы точек K’ и C’ определятся однозначно из условия сохранения простого отношения трех точек. Так что, если у четырехугольников отношение частей диагоналей было одинаковым, то точка C’ неизбежно спроектируется в точку, завершающую построение четырехугольника, подобного ABCD.
Следствие. Если основанием прямой призмы служит один из четырехугольников (из свойства 4), то среди плоских сечений можно найти четырехугольник, подобный второму (при достаточно большой высоте призмы).
Свойство 5. Свободной параллельной проекцией заданной трапеции может служить любая другая трапеция, имеющая то же отношение оснований.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.