Виды параллельных проекций. Изображение плоских фигур в свободной параллельной проекции. Теорема Польке-Шварца, страница 6

Характерной особенностью полных изображений является возможность однозначно определить на них взаимное расположение элементов, узнать, например, принадлежит ли точка заданной плоскости, найти общие точки прямых и т.д., т.е. фактически можно решать позиционные задачи.

Определение.  Позиционными  называются такие задачи на построение, где требуется определить взаимное расположение фигур в пространстве, находить их общие элементы.

     Пример 1. Даны точки A(A₁), B(B₁), C(C₁), определяющие некоторую плоскость, и отрезок MN(M₁N₁), определяющий вертикальную плоскость. Найти 1) линию пересечения плоскостей ABC и MNN₁M₁ (рис. 16); 2) точку пересечения прямой MN с плоскостью ABC.

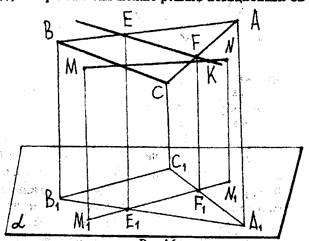
Рис.16

Решение. 1) Рассмотрим линию пересечения плоскости MNN₁M₁ с a - прямая M₁N₁.

Тогда M₁N₁ÇA₁B₁=E₁,

M₁N₁ÇA₁C₁=F₁.

Спроектируем точки E₁ и F₁ в плоскость ABC (точка EÎAB, FÎAC, т.к. E₁ÎA₁B₁, F₁ÎA₁C₁). Следовательно, EF - линия пересечения плоскостей ABC и MNN₁M₁, т.к. E₁F₁ - линия пересечения их проекций на основную плоскость a.

2) Для нахождения точки пересечения прямой MN и плоскости ABC достаточно:

а) найти линию пересечения плоскости ABC и плоскости MNN₁M₁, содержащей прямую MN -    прямая EF;

б) EFÇMN=K - искомая точка (т.к. EF и MN принадлежат одной плоскости MNN₁M₁, т.е. найдется их общая точка).

Замечание 2. Аналогичным образом можно найти точку пересечения прямых MM₁, NN₁, M₁N₁ с плоскостью ABC, она определяется из пересечения соответствующих прямых с прямой EF (рис. 16).

Пример 2. Найти линию пересечения плоскостей, определяемых треугольниками ABC(A₁B₁C₁) и FGH(F₁G₁H₁) (рис. 17).

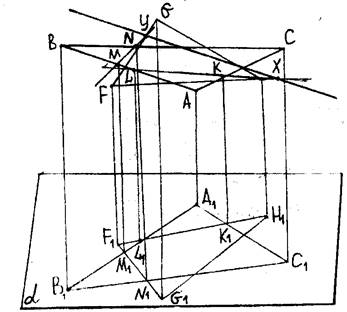
Рис.17

Решение. Используем вспомогательные (вертикальные) плоскости. Рассекая оба треугольника, определяем две прямые, которые принадлежат вертикальной плоскости и в пересечении дают точку, лежащую одновременно в плоскостях обоих треугольников. Двух таких точек достаточно для построения искомой прямой.

1) Найдем точку пересечения прямой FH с плоскостью ABC, для этого используем проектирующую плоскость FHH₁F₁ (пример 1)

F₁H₁ÇA₁B₁=K₁,

F₁H₁ÇA₁C₁=L₁.

Находим прообразы точек K₁ и L₁ на прямых AB и AC, получаем KL - линия пересечения плоскостей FHH₁F₁ и ABC.

Тогда KLÇFH=X - точка пересечения прямой FH с плоскостью ABC, т.е. точка, которая принадлежит как плоскости ABC, так и плоскости FGH.

2) Аналогично находим точку пересечения прямой FG с плоскостью ABC. Рассмотрим вертикальную плоскость GFF₁G₁

F₁G₁ÇA₁B₁=M₁,

F₁G₁ÇB₁C₁=N₁.

Точки M₁ и N₁ спроектируются в M и N на прямых AB и BC, MNÇFG=Y.

3) XY - линия пересечения плоскости ABC и плоскости FGH.

Замечание 3. Иногда плоскость на проекционном чертеже задают не тремя точками, а прямой l и точкой А(А₁), причем прямую удобно расположить в основной плоскости a (рис. 18). В этом случае очевидно, что заданная плоскость g пересекает основную по линии l, где l - след g.

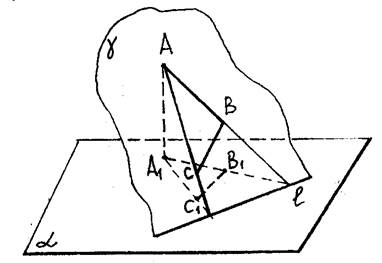
Рис.18

Оба способа задания плоскости на проекционном чертеже эквивалентны. Всегда можно в заданной плоскости g определить некоторый DABC. И наоборот: найдя точки пересечения прямых AB и A₁B₁, AC и A₁C₁, проведем через них след.

Замечание 4. При построении линий взаимного пересечения многогранников либо находят точки пересечения прямых одного тела с поверхностью второго (§5, пример 1(2)), либо рассматривают линии пересечения граней многогранников (§5, пример 2).

§6.  Построение плоских сечений многогранников.

Определение.  Плоским сечением (или просто сечением)  называют линию, состоящую из общих точек «секущей» плоскости и «рассекаемой» поверхности.

Замечание 19.  Чтобы построить сечение, нужно найти отрезки, по которым сечение рассекает грани, или точки, в которых сечение пересекается ребрами, т.е. может быть сведена к нахождению общих точек двух плоскостей (§5, пример 2), или прямой и плоскости (§5, пример 1).

Пример 1. Построить сечение пятиугольной призмы плоскостью, проходящей через 3 заданные точки M(M₁), N(N₁), P(P₁), лежащие на боковых ребрах (рис.19).

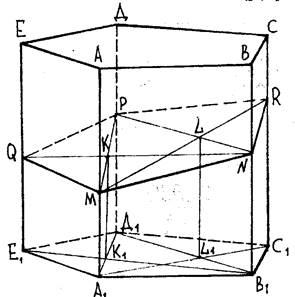
Рис.19