Решение. Выберем основную плоскость a - плоскость нижнего основания. Направление внутреннего проектирования зададим боковым ребром AA1. Тогда все точки заданы и изображение является полным. Найдем точки пересечения плоскости MNP(A1B1D1) с ребрами EE1 и CC1 (§5, пример 1)
1) B1E1ÇA1D1=K1.
2) Находим прообраз K точки K1 на прямой MP.
3) NKÇEE1=Q - точка пересечения ребра EE1 и секущей плоскости.
4) A1C1ÇB1D1=L1.
5) Прообразом точки L1 является точка LÎNP.
6) NLÇCC1=R - точка сечения ребра CC1 плоскостью MNP.
MQPRN - искомое сечение.
Замечание 2. Построения ничем не будут отличаться, если точки M,N,P будут заданы на гранях призмы.
Аналогичным образом строятся плоские сечения пирамид, но для удобства внутреннее параллельное проектирование заменяют центральным. При этом роль проектирующей плоскости будет играть любая плоскость, проходящая через вершину пирамиды (конуса).
Замечание 3. Рассмотренные в примерах задачи можно решить и другим способом, используя след секущей плоскости. Этот метод непригоден лишь в случаях удаления следа за пределы чертежа.
Пример 2. Построить сечение пятиугольной призмы, если заданы точки M(M1), N(N1), P(P1), где NÎBB1, M - середина AE1, PÎDD1 (рис. 20).
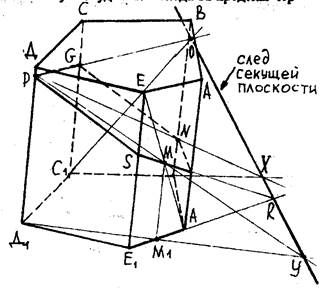
Рис.20
Решение. Для нахождения следа секущей плоскости определим две точки, ему принадлежащие. Они получены в пересечении прямых и их образов:
NPÇB1D1=X,
MPÇM1D1=Y,
XY - след секущей плоскости.
Найдем отрезок, по которому плоскость пересекает грань CC1D1D:
C1D1ÇXY=O,
OPÇCC1=G,
PG - линия пересечения грани CC1D1D и плоскости MNP.
Далее определяем линию пересечения грани AA1E1E и плоскости MNP:
A1E1ÇXY=R, RMÇEE1=S, RMÇAA1=T, ST - искомый отрезок, PSTNG - сечение призмы плоскостью MNP.
§7. Аксонометрические проекции. Частные случаи аксонометрии.
Рассмотрим свободную параллельную проекцию тройки декартовых осей Oxyz на некоторую плоскость p, получаем изображение этой тройки O1x1y1z1 (рис. 21). Пусть на осях заданы единичные отрезки ОА, ОВ, ОС; тогда (согласно теореме Польке, §3) любая тройка отрезков О1А1, О1В1, О1С1 может служить образом единичного репера.
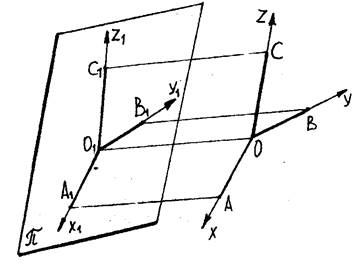
Рис.21
Введем числовые характеристики, определяющие отношения длин отрезков к длинам изображений:
![]() ,
, ![]() ,
, ![]() , где u, v, w -
коэффициенты (показатели) искажения длин по осям x, y, z.
, где u, v, w -
коэффициенты (показатели) искажения длин по осям x, y, z.
Если вместе с изображением осей (т.е. их аксонометрической проекцией) на плоскости p показана проекция точки M, которая связана с началом координат пространственной координатной ломаной линией OMxM’M1 (рис. 22) и заданы коэффициенты искажения u, v, w, то можно определить положение точки M в системе Oxyz:
![]() ,
, ![]() ,
, ![]() .
.
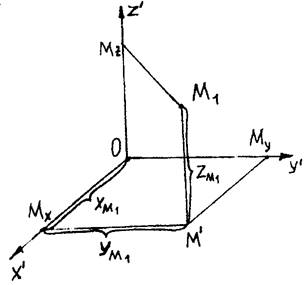
Рис.22
В этом смысле чертеж является метрически определенным, т.е. по нему вполне определяются расстояния между изображенными точками, т.е. размеры фигуры. Аксонометрический чертеж иногда называют однокартинным, т.к. аксонометрическая проекция получается в результате проектирования предмета на одну плоскость.
Определение. Аксонометрические проекции называют прямоугольными, если они получены в результате ортогонального проектирования на плоскость p. В противном случае их называют косоугольными.
В зависимости от соотношения между коэффициентами искажения по осям различают следующие аксонометрические проекции:
1) изометрические (если u=v=w),
2) диметрические (если равны только два числа, например u¹v=w),
3) триметрические (если u¹v¹w).
Перейдем к рассмотрению частных случаев аксонометрических проекций.
I. Косоугольная аксонометрия.
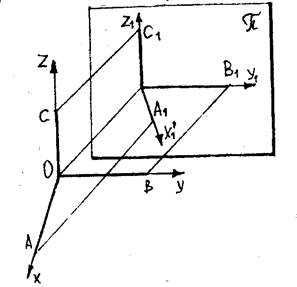
Рис.23
Наиболее часто используется диметрическая проекция, причем такая, когда плоскость p параллельна одной из координатных плоскостей, например, yOz (рис. 23). Тогда оси O1y1 и O1z1 изображаются в натуральную величину, как и любые фигуры, параллельные плоскости yOz, т.е. v=w=1. Третья ось O1x1 может быть расположена произвольно, однако в этом случае не всегда изображение будет наглядным. Такая проекция называется фронтальной.
Наибольшее распространение получила кабинетная фронтальная проекция, для которой
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.