Виды параллельных проекций. Изображение плоских фигур в свободной параллельной проекции. Теорема Польке-Шварца, страница 5

Замечание 2. Для того чтобы вписанная пирамида была правильной, достаточно взять в качестве ее вершины один из полюсов, а основание пирамиды вписать в сечение сферы, перпендикулярное оси NS. Выбор сечения, перпендикулярного оси NS не будет произвольным, если фигура, вписанная в сферу, наделена некоторым дополнительным условием. Например, вписать в сферу куб или правильный тетраэдр.

В заданиях такого типа полезно сразу выявить отношение , где h – высота фигуры, R – радиус окружности, описанной около основания искомой фигуры. Вычислив , мы однозначно определим угол при вершине осевого сечения вспомогательного конуса, т.е. конус описан около фигуры, вписанной в сферу, или используется для построения оснований цилиндра, вписанного в сферу.

     Пример 2. В заданную сферу вписать правильную четырехугольную пирамиду, если , где h - высота пирамиды, а - сторона основания.

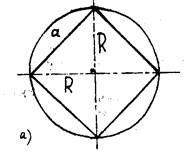
Рис.13, а

Решение. Необходимо найти h/R, поэтому выразим a через R (рис. 13, а), R - радиус окружности, описанной около основания.

a²=2R², , , , где e - произвольно выбираемый отрезок.

Строим отношение h/R, где , R=3e, определяем Ða (угол при вершине осевого сечения вспомогательного конуса), который прилежит к отрезку h.

.

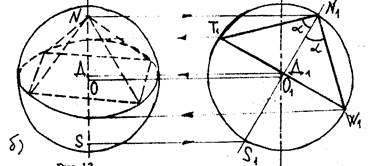
Рис.13, б

Далее переходим к основному построению (рис. 13, б). Пусть задана сфера, угол a откладываем влево и вправо от оси N₁S₁, считая один из полюсов вершиной пирамиды (например, полюс N), тогда вершина угла, равного 2a, тогда будет в точке N₁. Стороны угла в 2a продолжаем до пересечения с очертанием сферы в точках T₁ и W₁. Далее восстанавливаем конус на виде "спереди" и вписываем в него правильную 4-угольную пирамиду (§1), учитывая, что изображение должно быть наглядным.

Замечание 3. Для изображения правильной n-угольной призмы, вписанной в сферу, сначала определяют параметры цилиндра, вписанного в сферу и описанного около призмы. Рассмотрим вид "сбоку" (рис. 14). 

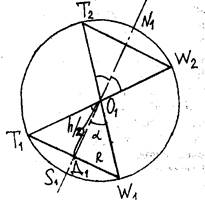
Рис.14

Выводим соотношение h к R, где h - высота призмы (цилиндра), R - радиус основания цилиндра. DOD₁W₁: ÐD₁OW₁=a, D₁O=h/2, D₁W₁=R, поэтому, выявив соотношение h/R, определим Ða, который затем отложим от оси N₁S₁ (с вершиной в точке О); на пересечении с очертанием сферы получаем точки T₁, W₁, T₂, W₂, где T₁W₁, T₂W₂ - вид «сбоку» оснований цилиндра. Далее восстанавливаем цилиндр и вписываем в него призму.

Замечание 4. Если в задаче необходимо описать около сферы произвольную n-угольную пирамиду с данным отношением h/a, то вначале определяем параметры вспомогательного конуса, который вписан в пирамиду и описан около сферы. Высота этого конуса равна высоте пирамиды, а радиус основания r нужно определить, выразив его через a (a - сторона основания пирамиды), т.е. найти a/r.

§5. Решение простейших позиционных задач.

Далее будем рассматривать изображения с точки зрения их определенности, полноты, когда однозначно можно выявить взаимное расположение элементов оригинала.

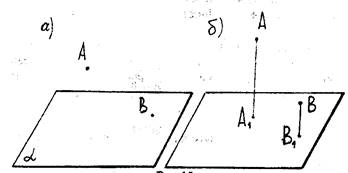
Рис.15

Так на рис.15,а мы не можем точно сказать: лежат точки А и В в плоскости a или находятся вне ее. Поэтому изображение является неполным.

Рис. 15,б в этом смысле - полный, т.к. ясно взаимное расположение всех трех его элементов: АÏa, ВÏa.

 Определение. Всякую точку А будем называть заданной на проекционном чертеже, если на нем изображена сама эта точка и ее параллельная проекция А₁ на некоторую плоскость a, которую назовем  основной.

Обозначение: А(А₁) (точка считается заданной).

 Определение. Изображение всякой фигуры на проекционном чертеже является полным, если каждая точка этой фигуры задана.

Для проверки полноты изображения нужно убедиться в том, что для каждой точки изображенной фигуры на чертеже указана или может быть найдена построением ее проекция на основную плоскость.

Замечание 1. Далее в каждом конкретном случае полнота изображения будет выявляться с помощью подходящего вспомогательного проектирования (параллельного или центрального), однако это проектирование должно быть общим для всех точек фигуры.