Виды параллельных проекций. Изображение плоских фигур в свободной параллельной проекции. Теорема Польке-Шварца, страница 4

(BDK)=(B’D’K’),

(ACK)=(A’C’M’).

Спроектируем тетраэдр A'B'C'D' на плоскость p₁, где  p₁ ^ K’M’. Обозначим эту прямоугольную проекцию A₁B₁C₁D₁ и заметим, что 

(B₁D₁K₁)=(BDK),

(A₁C₁K₁)=(ACK).

Построим прямую четырехугольную призму с верхним основанием A₁B₁C₁D₁ и с нижним - A₂B₂C₂D₂. Согласно следствию 1 свойства 4: среди плоских сечений построенной призмы найдется четырехугольник, имеющий форму заданного ABCD.

Т.е. если обозначим плоскость этого сечения w, то проектирование тетраэдра на плоскость w дает исходную форму ABCD.

Теорема доказана.

Следствие (теорема Польке). Любые три выходящие из одной точки отрезка, не лежащие все на одной прямой, могут служить параллельной проекцией пространственного репера прямоугольной декартовой системы координат.

Доказательство основано на теореме Польке-Шварца, т.к. пространственный репер можно считать частью тетраэдра.

Замечание. Теорема Польке-Шварца дает простые правила для построения изображений пирамид, призм, а так же их предельных обобщений - конусов и цилиндров.

§4.  Изображение сферы и  фигур, вписанных в сферу и описанных около нее.

Плоскость, проходящая через центр сферы, пересекает сферу по окружности, которая называется экватором (рис.11, а). Перпендикулярно плоскости экватора располагается ось сферы, пересекающая ее в двух точках: N - северный полюс, S  - южный полюс.

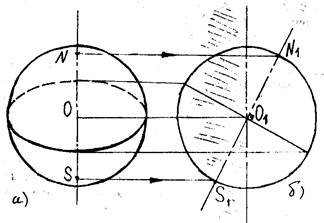
Рис.11

Снабдим изображение сферы ее видом "сбоку" (рис.11, б), который получен рассечением сферы вертикальной проектирующей плоскостью, проходящей через ось NS сферы. Затем поворачиваем срез шара до совмещения с плоскостью проектирования.

Экватор, видимый "спереди" как эллипс,  на виде "сбоку" представлен отрезком, перпендикулярным оси сферы.

Отрезок N₁S₁ на виде "сбоку" представляет натуральную величину отрезка NS.

Для удобства рассуждений впредь будем считать плоскость проектирования w проходящей через центр сферы, поэтому одна полусфера (видимая) лежит над чертежом, вторая (невидимая) - под чертежом. На виде "сбоку" плоскость чертежа совпадает с вертикальной осью симметрии. Она разделяет все точки сферы на видимые (справа) и невидимые (слева) (рис.11, б).

Все точки проектируются на вид "сбоку" с вида "спереди", и наоборот, параллельно прямой ОО₁.

Особенностью изображения сферы и связанных с ней фигур (вписанных или описанных) является то, что все изображения здесь метрически определенные, т.е. по чертежу можем восстановить реальные размеры изображенных фигур.

 Изображение сферы считается заданным, если показано ее очертание и полюсы N, S.

     Пример 1. Дано изображение сферы и точка D, лежащая на оси сферы. Построить сечение шара с центром в точке D, параллельное плоскости экватора.

     Решение. Изображаем вид "сбоку". Спроектируем точки N, S и D на вид "сбоку" вдоль прямой ОО₁ (рис. 12). Строим сечение на виде "сбоку", проходящее через точку D₁, для этого проводим прямую T₁W₁, проходящую через точку D₁, перпендикулярно N₁S₁.

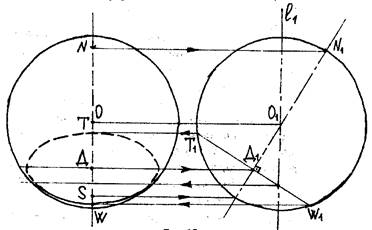
Рис.12

Всякая параллель сферы на виде "сбоку" изображается отрезком, перпендикулярным отрезку N₁S₁,  а на виде "спереди" - эллипсом.  Для построения этого эллипса достаточно найти его большую и малую оси.

Малая ось определяется крайними точками T₁,W₁ параллели на виде "сбоку" (эти точки проектируются параллельно прямой ОО₁ на прямую NS). Большая ось эллипса равна по величине диаметра T₁W₁ параллели. Изображение параллели может содержать видимую и невидимую части, которые стыкуются на  очертании сферы. Точка стыковки на виде "сбоку" будет в пересечении параллели с осью симметрии  l₁, на виде "спереди" эта точка лежит на очертании сферы и является точкой касания очертания с эллипсом.

Замечание 1. При построениях, связанных со сферой, можно отказаться от двух изображений "спереди" и "сбоку", выполняя все рисунки внутри одной окружности.