Математика \ Алгебра

Виды параллельных проекций. Изображение плоских фигур в свободной параллельной проекции. Теорема Польке-Шварца, страница 13

3.3

F1ÇF2

1

5

9

2

6

10

3

7

11

4

8

12

Таблица 4 (продолжение)

3.3

F1ÇF2

13

17

21

22

14

18

23

15

19

24

16

20

25

Таблица 5

№

4.2

вар.

Ф

1

четырехугольная прямая призма, в основании которой лежит ромб с острым углом 60о

2

правильная четырехугольная пирамида

3

правильная треугольная призма

4

правильная усеченная шестиугольная пирамида, отношение сторон верхнего и нижнего основания которой 1:2

5

четырехугольная прямая призма, в основании которой лежит ромб с острым углом 45о

6

правильная треугольная  пирамида

7

четырехугольная пирамида, в основании которой лежит ромб с острым углом 30о

8

правильная восьмиугольная призма

9

треугольная призма, в основании которой лежит прямоугольный равнобедренный треугольник (гипотенуза параллельна Oy)

10

правильная восьмиугольная пирамида

11

правильная шестиугольная призма

12

четырехугольная пирамида, в основании которой лежит ромб с острым углом 60о

13

треугольная пирамида, в основании которой лежит прямоугольный равнобедренный треугольник (гипотенуза параллельна Oy)

14

правильная четырехугольная призма

15

треугольная  прямая  призма, в основании которой лежит равнобедренный треугольник с углом 120о

16

правильная усеченная треугольная пирамида, отношение сторон верхнего и нижнего основания которой 1:2

17

четырехугольная прямая призма, в основании которой лежит ромб с острым углом 45о

18

правильная пятиугольная  пирамида

19

прямоугольный параллелепипед, третье измерение которого равно 3

20

правильная усеченная восьмиугольная пирамида, отношение сторон верхнего и нижнего основания которой 2:3

21

правильная шестиугольная призма

22

правильная усеченная шестиугольная пирамида, отношение сторон верхнего и нижнего основания которой 1:4

23

правильная шестиугольная пирамида

24

правильная пятиугольная призма

25

правильная усеченная четырехугольная пирамида, отношение сторон верхнего и нижнего основания которой 1:3

Таблица 6

4.3

W

Список литературы.

1) Атанасян Л.С., Базылев В.Т. Геометрия. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов. В 2 ч. Ч.2. - М.: Просвещение, 1987. - 352 с.; ил.

2) Атанасян Л.С., Васильева М.В., Вересова Е.Е. и др. Сборник задач по геометрии. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов, ч.II. - М.: Просвещение, 1975.

3) Ботвинников А.Д. и др. Черчение: Учеб. для 6-7 кл. сред. общеобразоват. шк./ А.Д.Ботвинников, В.Н.Виноградов, И.С.Вышнепольский. - М.: Просвещение, 1988. - 224 с.: ил.

4) Виноградов В.Н. Начертательная геометрия. Минск, «Вышайш. школа», 1977.

5) Вывальнюк Л.Н., Шефтель З.Г., Рафаловский Э.В. Математика: Пособие для факультатив. занятий в 9 кл. - К.: Рад. шк., - 1984. - 136 с.

6) Панкратов А.А. Начертательная геометрия. Пособие для студентов пед. ин-тов. Изд.-е  второе. М.: Государственное учебно-педагогическое издательство министерства Просвещения РСФСР, 1963.

7) Фролов С.А. Начертательная геометрия: Учебник втузов. - М.: Машиностроение, 1978. - 240 с., ил.


1)

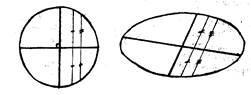
Сопряженными называются такие диаметры эллипса (окружности), каждый из которых проходит через середины хорд, параллельных другому диаметру (из определения следует и способ построения сопряженных диаметров).

Скачать файл