Решение многокритериальной задачи о назначениях, страница 22

Полученное выше противоречие означает, что при
переходе от матрицы М к матрице `М одна часть ин­
формации позволила определить, что субъект С_i ближе к объекту O_j, чем субъект С₁ а другая часть ин­
формации определяла прямо противоположное. По
условию теоремы линейные порядки непротиворечивы,
 что позволяет сделать вывод о  наличии хотя бы
одной клетки D₁/D₁ на пересечениях строк С₁ ,С_i и
столбцов O_v, O_j.                  

В общем случае в графе `T_j индекс D₁ может иметь иная вершина, чем С_1j.

Тогда такое же противоречие возникнет позже, когда вершина графа `T<sub>k</sub> с индексом D<sub>1</sub> окажется в уже встречавшейся р-й строке или вер­шина графа `S_p окажется в уже встречавшемся k-м столбце. Так как общее число строк и столбцов мат­рицы  ` `M`(с чертой) равно 2n, тоуказанноепротиворечие встре­тится не позднее чем через 2п шагов. Очевидно, что противоречие устраняется при наличии хотя бы одной клетки D₁/D₁ на пересечениях встречавшихся строк и столбцов, что и требовалось доказать.

        Общий алгоритм решения многокритериальной задачи о назначениях

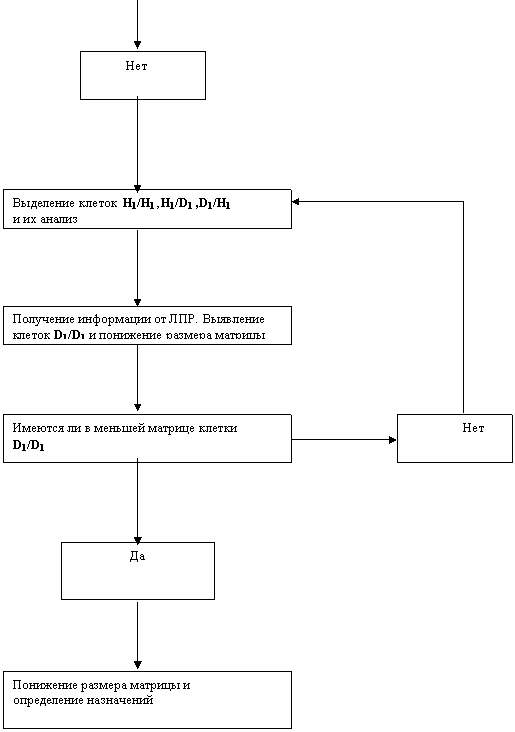
Результаты, изложенные в предыдущих разделах, позволяют предложить общий алгоритм решения мно­гокритериальной задачи о назначениях, блок-схема которого приведена на рис. 3.

 

 

Как уже указывалось, первый этап решения зада­чи— формальный анализ — состоит из построения графов подобии T_v, S_m и матрицы сходства М. При анализе матрицы М определяются очевидные назна­чения, соответствующие клеткам D₁/D₁, если тако­вые существуют. При определении очевидных назна­чений происходит понижение размерности матрицы М, после чего снова ищутся очевидные назначения.