Эта формула выведена с учетом действия только крутящего момента. В действительности же, кроме крутящего момента, в сечении стержня пружины возникает изгибающий момент, поперечная сила и продольная сила.
Сравнивая величины осадки пружины, полученные опытным путем и аналитически, можно оценить влияние параметров, не учтенных при выводе формулы, на деформацию пружины. Осадка пружины λ должна находится в линейной зависимости от нагрузки F. Чтобы подтвердить выше сказанное, нужно по величинам измеренных на опыте деформаций пружины построить диаграмму сжатия пружины в ортогональной системе координат λ - F (рис 8.2).
Кроме определения деформации пружины, в ходе опыта нужно определить максимальные касательные напряжения, возникающие в поперечном сечении витка пружины. Они вычисляются по формуле:
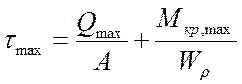(8.2)
где
, а 
.Зная величины напряжений 
от поперечной силы, 
от крутящего момента и суммарные
напряжения 
, нужно построить соответствующие
эпюры напряжений (рис.8.3).
|
|
|
Рис. 8.2 |
|
|
|
Рис. 8.3 |
В выводах необходимо отметить: подтверждается ли закон Гука для пружины на опыте, в какой точке сечения пружины возникают наибольшие касательные напряжения (с учетом поперечной силы), можно ли в данном случае использовать приближенную формулу для вычисления наибольших касательных напряжений.
1. В каких точках винтовой пружины возникает максимальное касательное напряжение? Как его подсчитать?
2. По какой формуле производилось теоретическое определение осадки пружины.
3. Какие гипотезы были приняты при выводе формулы для определения осадки пружины.
ИССЛЕДОВАНИЕ НАПРЯЖЕННОГО СОСТОЯНИЯ ПРИ ИЗГИБЕ СТАЛЬНОЙ БАЛКИ ДВУТАВРОВОГО СЕЧЕНИЯ
Цель работы: изучение закона распределения нормальных напряжений в поперечном сечении балки и определение величин и направлений главных напряжений в одной из точек.
Из теории плоского поперечного изгиба известно, что в сечении балки, перпендикулярном к ее оси, возникают нормальные и касательные напряжения, которые подсчитываются по формулам
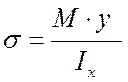и 
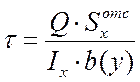(9.1)
Первая из приведенных формул выводилась для случая
чистого изгиба, когда в сечении стержня действует только изгибающий момент, а поперечная
сила отсутствует и, следовательно, 
. Кроме того, в
качестве исходных предпосылок были приняты следующие гипотезы:
1. Сечения, плоские и перпендикулярные оси стержня до деформации остаются плоскими и перпендикулярными оси и после деформации (рис. 9.1).
2. Если изгибаемый стержень мысленно расчленить на волокна, расположенные вдоль оси стержня, то эти волокна не будут оказывать давления друг на друга, а будут испытывать только деформацию растяжения или сжатия.
3. Материал изгибаемого стержня - абсолютно упругий и подчиняется закону Гука.
|
|
|
Рис. 9.1 |
Последнее допущение положено в основу вывода всех формул для определения напряжений в теории сопротивления материалов.
Первые две гипотезы, со ссылкой на результаты экспериментальных наблюдений над изгибаемыми балками, принимаются именно в теории изгиба.
Как показывают более строгие исследования методами
теории упругости, в случае чистого изгиба принятые допущения (гипотезы) согласуются
с истиной. Однако теория изгиба в сопротивлении материалов не останавливается
на приведенных выше гипотезах: в ней, опять же со ссылкой на экспериментальные
и теоретические исследования, утверждается, что формулу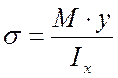 
,
выведенную для случая чистого изгиба, можно без существенной погрешности
использовать при подсчете нормальных напряжений при поперечном изгибе, когда
поперечная сила 
не равна нулю. Однако
оказывается, что ни первая, ни вторая гипотезы, строго говоря, не верны.
Сечения балки при поперечном изгибе, когда 
,
не остаются плоскими и продольные волокна давят друг на друга, т.е. 
(рис.9. 2).
|
|
|
Рис. 9.2 |
При
выводе формулы Журавского для определения касательного напряжения в случае
поперечного изгиба используется зависимость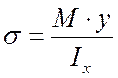 
и,
следовательно, принимаются все связанные с ней и перечисленные выше допущения.
Кроме того дополнительно предполагается, что касательные напряжения по ширине
сечения распределены равномерно.
Таким образом, приведенные вначале теоретические формулы (9.1) для определения нормального и касательного напряжений при изгибе балки опираются на ряд допущений и приближений, справедливость которых подтверждается экспериментально.
Далее, согласно теории изгиба, элемент, вырезанный из боковой поверхности балки, испытывает в общем случае плоское напряженное состояние такого вида, как это показано на рис.9.3.
|
|
|
Рис. 9.3 |
При этом 
и 
подсчитываются по формулам (9.1),
нормальные напряжения на площадках, параллельных продольной оси балки, согласно
гипотезе (2) приняты равными нулю. Тогда главные напряжения в данной точке
балки и их ориентация определяются зависимостями:
, 
.
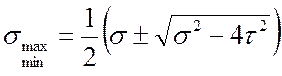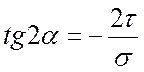Очевидно, что на величину и направление теоретически найденных главных напряжений оказывают влияние все те допущения, о которых говорилось выше.
Сравнение опытных данных с теоретическими позволит дать оценку достоверности принятых в теории гипотез и допущений.
В качестве объекта исследования избрана стальная балка двутаврового сечения (рис.9.4). Ожидаемый вид эпюры нормальных напряжений в сечении – линейный, поэтому в опыте рекомендуется измерение производить не менее чем в 5 точках по высоте сечения.
|
|
|
|
Рис. 9.4,а |
Рис. 9.4,б |
Для экспериментального определения величины и направления главных напряжений необходимо воспользоваться по крайней мере тремя измерениями упругих деформаций в заданной точке плоско напряженной стенки балки (рис.9.4,а, точка Б).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
