По
найденным опытным путем с помощью розетки из трех тензодатчиков значениям ![]() надо найти величину и направление
главных деформаций и напряжений. Выведем для этого необходимые расчетные формулы.
надо найти величину и направление
главных деформаций и напряжений. Выведем для этого необходимые расчетные формулы.
По известной из теории деформированного состояния зависимости можно написать:
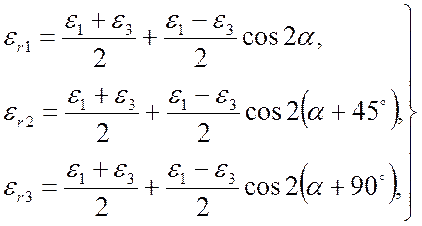 (9.2)
(9.2)
где
![]() и
и ![]() -
главные деформации.
-
главные деформации.
При этом
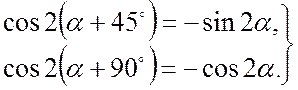 (9.3)
(9.3)
Решая
систему трех уравнений (9.2) относительно ![]() ,
, ![]() и
и ![]() с
учетом (9.3), нетрудно найти
с
учетом (9.3), нетрудно найти
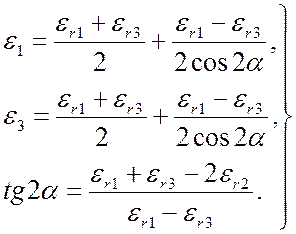 (9.4)
(9.4)
В
процессе вывода использовался рисунок 9.8, на котором угол ![]() отложен по ходу часовой стрелки от
направления
отложен по ходу часовой стрелки от
направления ![]() . Следовательно, положительное
значение угла
. Следовательно, положительное
значение угла ![]() , полученное из последнего
выражения в (9.4), надо отсчитать от
, полученное из последнего
выражения в (9.4), надо отсчитать от ![]() по часовой стрелке.
по часовой стрелке.
|
|
|
Рис. 9.8 |
Таким
образом, по зависимости (9.4), основываясь на измерениях трех тензодатчиков в
розетке, можно найти направление и величину главных деформаций ![]() и
и ![]() .
Главные напряжения можно выразить через главные деформации из зависимостей
обобщенного закона Гука применительно к плоскому напряженному состоянию:
.
Главные напряжения можно выразить через главные деформации из зависимостей
обобщенного закона Гука применительно к плоскому напряженному состоянию:
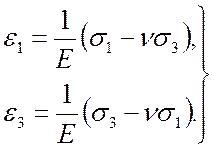 (9.5)
(9.5)
Умножив вторую строку на ν и сложив с первой, получим
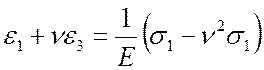 ,
,
откуда
найдем ![]() . Выражение
. Выражение ![]() можно
получить аналогично.
можно
получить аналогично.![]()
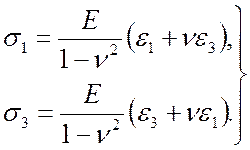 (9.6)
(9.6)
Как
видно из рис. 9.8, угол ![]() между осью балки
z и направлением одного из главных напряжений выразится зависимостью
между осью балки
z и направлением одного из главных напряжений выразится зависимостью
![]() .
.
Теоретические расчеты
Для теоретического определения напряжений в сечении "m-n" и в точке Б исследуемой балки необходимо прежде всего построить эпюры изгибающего момента М и поперечной силы Q.
Нормальные напряжения в точках 1-5 сечения "m-n" определяются зависимостью
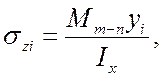
где
·
![]() -
координата точек
-
координата точек ![]() , в которых определяются
напряжения в поперечном сечении балки;
, в которых определяются
напряжения в поперечном сечении балки;
·
![]() -
изгибающий момент в сечении "m-n" исследуемой балки.
-
изгибающий момент в сечении "m-n" исследуемой балки.
В
точке Б на площадке, перпендикулярной оси балки, подсчитываются ![]() и
и ![]() :
:
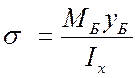 ,
, 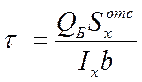 ,
,
где![]() и
и ![]() -
изгибающий момент и поперечная сила в сечении балки, в котором расположена
точка Б. Напряжения, действующие на площадках элемента, вырезанного в
окрестности точки Б, показаны на рис.9.9.
-
изгибающий момент и поперечная сила в сечении балки, в котором расположена
точка Б. Напряжения, действующие на площадках элемента, вырезанного в
окрестности точки Б, показаны на рис.9.9.
Величину главных напряжений в точке Б найдем по формуле:
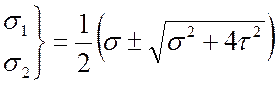 .
.
Их ориентация по отношению к оси балки определяется зависимостью
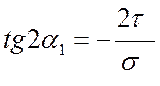 ,
,
где положительное значение ![]() откладывается
против хода часовой стрелки от оси балки z.
откладывается
против хода часовой стрелки от оси балки z.
|
|
|
Рис. 9.9 |
Сравнение результатов
Значение нормальных напряжений в пяти точках сечения балки, найденные экспериментально и подсчитанные теоретически, выписываются в сводную таблицу. Туда же заносятся определенные экспериментально и подсчитанные теоретически значения главных напряжений в точке Б и угла наклона одной из главных площадок по отношению к продольной оси балки.
Подсчитывается в процентах расхождение
между теоретическими и экспериментальными значениями напряжений ![]() (при
(при ![]() ),
),
![]() ,
, ![]() и
угла
и
угла ![]() . Строится теоретическая эпюра
. Строится теоретическая эпюра ![]() в сечении "m-n" и на нее накладывается экспериментальная.
в сечении "m-n" и на нее накладывается экспериментальная.
Выводы должны содержать оценку того, насколько хорошо согласуются экспериментальные наблюдения с гипотезой плоских сечений, подтвердится ли закон Гука, удовлетворительно ли согласуются теоретические и опытные значения напряжений в сечении "m-n", главные напряжения и их ориентация в точке Б балки.
1. Какова цель опыта?
2. Какие измерения производились во время опыта, и какие приборы для этой цели применялись?
3. Опишите расчетную схему балки и нагрузки?
4. Почему нагружение балки производилось ступенями?
5. Какие гипотезы были положены в основу при выводе зависимости для определения нормального напряжения при изгибе балки?
ОПРЕДЕЛЕНИЕ ЦЕНТРА ИЗГИБА В СЕЧЕНИИ БАЛКИ С ТОНКОСТЕННЫМ НЕЗАМКНУТЫМ ПРОФИЛЕМ
Цель работы: экспериментально убедиться в существовании центра изгиба, найти его положение и сравнить с теоретическим.
В теории изгиба стержней при выводе формул нормальных и касательных напряжений предполагалось, что сечение стержня симметрично и внешняя нагрузка прикладывается к центральной оси стержня в плоскости его симметрии. При этих условиях в стержне действительно возникает только деформация плоского изгиба. Как показано в теории, картина несколько меняется, если поперечное сечение стержня имеет форму тонкостенного профиля, несимметричного относительно плоскости приложения внешней нагрузки. В этом случае в поперечном сечении возникают касательные напряжения, как бы обтекающие контур сечения, и создающие относительно центра тяжести сечения С момент касательных усилий (рис.10.1).
|
|
|
Рис. 10.1 |
В связи с этим введено новое понятие – центра изгиба. Центр изгиба А – точка в плоскости сечения стержня, относительно которой главный момент всех касательных усилий в поперечном сечении равен нулю (рис. 10.1). Заметим, что в сечениях с одной осью симметрии, центр изгиба А расположен обязательно на этой оси. В сечении же с двумя осями симметрии – центр изгиба лежит на их пересечении, т.е. его положение совпадает в этом случае с центром тяжести сечения.
Если линия действия внешней нагрузки проходит через центр изгиба, то касательные усилия (согласно определению) и внешняя нагрузка относительно точки А дадут в плоскости сечения момент, равный нулю. Следовательно, кручения не возникнет, и стержень будет испытывать только плоский изгиб.
На основании этого сделано обобщение: деформация плоского изгиба наблюдается, когда внешняя нагрузка приложена к стержню в плоскости, проходящей вдоль стержня через центры изгибов сечений параллельно одной из главных центральных осей инерции поперечного сечения (на рис.10.1 это направление отмечено линией, проходящей через центр изгиба А).
Постановка опыта
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.