Методические рекомендации к выполнению лабораторных работ по дисциплине "Сопротивление материалов". Часть 1, страница 13

Отсюда следует практический вывод: если мы будем исследовать балки с малым отношением , т.е. достаточно гибкие, и получим удовлетворительные результаты при применении приближенного дифференциального уравнения вплоть до предельного по условию прочности значения 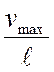, то  сможем утверждать, что для менее гибких балок  приближенное дифференциальное уравнение должно давать так же удовлетворительные результаты.

Определение прогибов балки, заделанной одним концом.

Постановка опыта

Исследуется балка в виде консоли (рис.11.1), прямоугольного поперечного сечения с размерами  и . Загружение производится на расстоянии  от заделки, а прогиб определяется по промежуткам между наколами, делаемыми на щитке  с миллиметровкой. Расстояние от F до конца иглы равно с. Относительная жесткость балки достаточно мала , а следовательно, податливость велика.

Рис. 11.1

Чтобы установить максимальную нагрузку для этой балки по условию прочности, запишем:

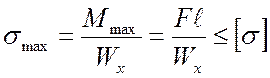, или

Отсюда 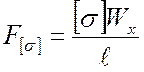, или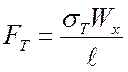

Выберем  так, чтобы оно было более , но не превышало :  ,

назначив  (желательно целое число), найдем , которое будет соответствовать этой нагрузке: 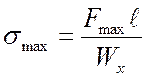. Нагрузка прикладывается равными ступенями от нуля  до  .

Проведение опыта

Последовательность выполнения опыта следующая.

На щитке  (рис.11.1) устанавливается и выравнивается по отвесу листок миллиметровки. Делаются все необходимые измерения размеров балки: по длине – с точностью до 1 мм, поперечное сечение – с точностью до 0,1 мм.

Без нагрузки делается первый накол на миллиметровке. Затем нагрузка увеличивается равными ступенями,  и каждый раз аккуратно делается новый накол на миллиметровке. Так продолжается до нагрузки . После этого производится полная разгрузка балки. Необходимо проверить, приходится ли игла, расположенная на балке, против первого  накола. Это свидетельствует о том, что в процессе опыта миллиметровка не была сбита, и деформации в балке были только упругие. Если игла не возвратилась к первоначальной точке накола, то опыт необходимо повторить.

Результаты опыта

По миллиметровке измеряется расстояние от первой точки до каждой из последующих. Эти величины дают прогибы конца консоли от соответствующей нагрузки. Результаты измерений заносятся в таблицу.

Теоретические подсчеты

Для схемы балки, изображенной на рис.11.1, необходимо подсчитать прогиб конца консоли в функции от F. Используем для решения этой задачи метод начальных параметров. Расположим начало координат в заделке (рис.11.2).

Рис. 11.2

При ,  ,  , , ,

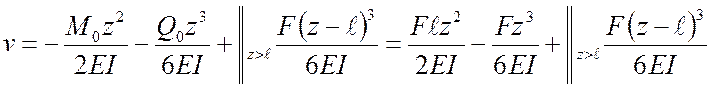
При ,

.

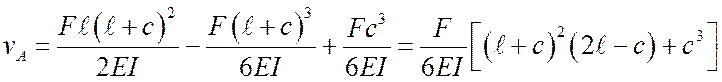Учитывая малость величины с по сравнению , вторым слагаемым в квадратной скобке можно пренебречь:

,

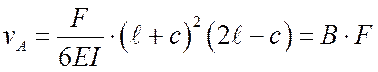где .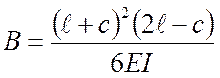

После подсчета коэффициента B можно заполнить таблицу теоретических значений .

По табличным данным следует построить графики изменения ,  ,  в функции от F. Здесь δ – расхождение в процентах между  и  ;

.

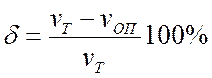В выводах необходимо оценить возможность применения приближенного дифференциального уравнения изогнутой оси при определении прогибов применительно к балкам исследованной и большей жесткости во всем диапазоне упругих деформаций.

Контрольные вопросы.

1.  Какие допущения были использованы при получении приближенного дифференциального уравнения изогнутой оси балки?

2.  В каком сечении балки на опыте производилось измерение прогибов?

3.  Почему нагружение балки производилось ступенями?

4.  Как определялась максимальная внешняя нагрузка  для заданной балки?

5.  Как влияет отношение  на возможную величину наибольшего относительного прогиба ?

Лабораторная работа № 12.

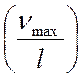ОПРЕДЕЛЕНИЕ ПРОГИБОВ ГИБКОЙ БАЛКИ НА ДВУХ ОПОРАХ, ПОДВЕРГНУТОЙ ЧИСТОМУ ИЗГИБУ

Цель работы: экспериментальная оценка границ применимости приближенного и точного дифференциального  уравнения изогнутой оси к  балке большой гибкости.

Постановка опыта

Схема балки представлена на рис.12.1.

Рис. 12.1

Исследованию подлежат прогибы на участке между опорами, на котором балка подвергается чистому изгибу. Сама балка сделана из стальной линейки толщиной приблизительно 1 мм. Отношение высоты балки к пролету составляет , что указывает на малую жесткость и большую податливость балки.

Как можно видеть из рис.12.1, при большой податливости балки, больших углах поворота на опорах, плечо силы F, первоначально равное a, не остается постоянным, оно убывает с ростом деформации. Изгибающий момент на участке балки , первоначально равный , перестает быть линейной функцией от нагрузки F.

Для устранения этого недостатка  видоизменена загружающая часть балки. Консоли a сделаны жесткими (рис.12.2). На них укреплены изогнутые по дуге окружности с радиусом a сегменты. Поддоны для грузов подвешиваются с помощью тросиков, закрепленных в самой верхней точке сегментов. При нагружении такой системы будет происходить изгиб балки, поворот консоли с сегментами, но плечо груза F относительно опор остается неизменным, равным a. Учитывая малую жесткость балки, для уравновешивания утяжеленных консолей сделаны специальные контргрузы.

Рис. 12.2

В середине пролета   установлена шкала, по которой берутся отсчеты для определения прогиба в процессе загружения балки.

Чтобы установить максимальную нагрузку для этой балки, воспользуемся условием прочности и, приняв  и  подобно тому, как это делалось предыдущем опыте, подсчитаем

; .

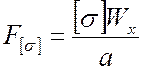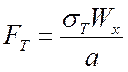Назначим  так, чтобы .

Проведение опыта

Последовательность выполнения опыта проста. Нагрузка на поддонах увеличивается ступенями. По шкале (см. рис.12.2) определяется прогиб в середине пролета. Процесс продолжается до тех пор, пока нагрузка на поддонах не достигает .

Однако проведение опыта требует особой тщательности и аккуратности. Ввиду большой гибкости балки в ходе опыта наблюдаются большие перемещения подвижной опоры балки. Небольшие перекосы, случайные препятствия, силы трения в системе могут заметно сказаться на результатах опыта и внести дополнительную погрешность в измеряемую величину прогиба. Поэтому как перед опытом, так и на каждой ступени нагрузки, следует проверить, не препятствует ли что-либо деформации балки. Достигается эта проверка легким колебанием системы около положения равновесия после каждого изменения нагрузки.