Теоретическое и экспериментальное изучение работы растянутых (сжатых) стержней с различного рода ослаблениями поперечных сечений показывает, что вблизи этих ослаблений возникает резкая неравномерность в распределении напряжений, характеризующаяся существенным повышением их значений (рис. 5.2,а). С этим нельзя не считаться при расчете и проектировании конструкций, в состав которых входят стержни с ослаблениями.
Условное напряжение, определяемое, как отношения усилия N в стержне к фактической площади его поперечного сечения в месте ослабления назовем номинальным:
,
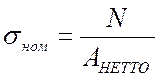(5.6)
где 
определяется как
разность между площадью поперечного сечения стержня без учета ослабления и
площадью ослабления
. (5.7)
|
|
|
Рис. 5.2,а Рис. 5.2,б |
Основной характеристикой
неравномерности распределения напряжений в зоне ослабления сечения является
коэффициент концентрации напряжений 
, представляющий
собою отношение максимального напряжения в зоне очага концентрации 
к номинальному:
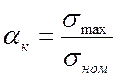(5.8)
Если значение 
легко может быть получено
теоретически, то определение величины (особенно
в случае ослаблений сложной конфигурации) проще всего осуществить с помощью
описанного выше поляризационно-оптического метода. Обработка результатов
эксперимента в этом случае очень проста, потому что нет необходимости в
разделении главных напряжений, так, как заранее известно, что главное
напряжение, действующие по нормали к свободному контору, равно нулю.
Принцип Сен-Венана
Значительная концентрация напряжений наблюдается и в месте приложения внешней нагрузки. По мере удаления от этого места напряжения, затухая, выравниваются (рис. 5.2,б). При учете этого обстоятельства руководствуются принципом Сен-Венана (французский ученый–механик). Согласно этому принципу на некотором расстоянии от места приложения нагрузки, распределение напряжений практически не зависит от характера приложения нагрузки, а только от ее равнодействующей.
Особенности приложения нагрузки к растянутому (сжатому) стержню (не тонкостенному) проявляются, как правило, на расстоянии, не превосходящем генерального размера поперечного сечения.
Результаты опыта.
Ознакомление с поляризационно-оптическим методом проводится с применением проекционно-поляризационной установки (ППУ), принцип действия которой изложен ранее (рис.5.1)
Зарисовываются схемы исследуемых образцов и картины полос изохром для двух – трех образцов (по указанию преподавателя) (рис.5.3,а).
Образец, изображенный на рис.5.3,б служит для иллюстрации принципа Сен-Венана.
Выводы. На основании полученных картин изохром устанавливаются наиболее опасные виды ослаблений (поперечная щель, треугольное отверстие, ступенчатый переход от одного сечения к другому), наблюдается положительный эффект от придания плавного перехода от сечения к сечению, выделяются зоны, в которых предположение о равномерном распределении напряжений является несправедливым.
|
|
|
|
Рис. 5.3,а |
Рис. 5.3,б |
На примере исследования образца на рис.5.3,б устанавливается справедливость принципа Сен-Венана.
1. Из каких материалов изготовлены образцы для проведения опытов?
2. Опишите методику проведения опыта.
3. Сформулируйте принцип Сен-Венана и укажите на образцах зоны его действия.
4. Какие виды ослабления сечения являются наиболее опасными с точки зрения напряженного состояния?
Цель работы: определение модуля упругости при сдвиге, проверка на опыте закона Гука при кручении.
Для испытания образцов на кручение применяются машины, на которых можно создать и измерить крутящий момент в испытываемом образце.
В опыте используется стальной образец круглого поперечного сечения диаметром d = 15÷20 мм и расчетной длиной l (см. рис. 6.1). Согласно стандарту, она равна десяти диаметрам l= 10d.
|
|
|
Рис. 6.1 |
В ходе эксперимента определяется угол закручивания образца на расчетной длине l. Для этого определяются углы поворота в сечениях А и В. Способы их определения могут быть различны.
Выполнение опыта
Эксперимент начинают с измерения диаметра образца, определения расчетной длины l, подсчета момента инерции Iр и момента сопротивления Wр. Размеры образца, его геометрические характеристики и данные о материале заносятся в журнал лабораторных работ.
Крутящий
момент в процессе загружения увеличиваем равными ступенями на величину 
.
Приращение отсчетов ΔА и ΔВ есть углы поворотов соответствующих сечений, увеличенные в К раз. Разность приращений (ΔА-ΔВ) есть угол закручивания образца на длине l, от приращения крутящего момента ΔМкр, увеличенный в К раз. Коэффициент увеличения К зависит от способа определения углов поворота. Величина угла закручивания определяется по формуле
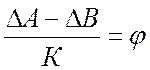(6.1)
Принятая методика выполнения эксперимента, а именно последовательное загружение образца ступенями, равными ΔМкр, дает возможность проверить на опыте справедливость закона Гука при кручении. Если угол закручивания по мере нарастания крутящего момента изменяется линейно, то можно сказать – материал образца подчиняется закону Гука.
На
основании произведенных в процессе опыта измерений строится диаграмма кручения
в системе осей 
.(рис.6.2).
|
|
|
Рис. 6.2 |
Величину модуля сдвига G можно вычислить по формуле:
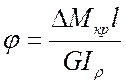(6.2)
Величины
, входящие в формулу (6.2), известны.
Угол закручивания 
определяется из опыта.
Из формулы (6.2) находим модуль сдвига
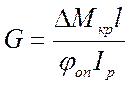(6.3)
Модуль сдвига можно определить и теоретически, пользуясь формулой:
,
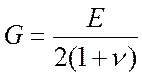(6.4)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
