Методические рекомендации к выполнению лабораторных работ по дисциплине "Сопротивление материалов". Часть 1, страница 14

Прогибы, найденные на каждой новой ступени нагрузки, записываются в журнал наблюдений.

Теоретическое определение прогибов

Сначала определим прогибы с помощью приближенного дифференциального уравнения изогнутой оси.

Применим метод начальных параметров. Расчетную схему балки примем в виде балки с шарнирными опорами по концам (рис.12.3).

Рис. 12.3

Действие отброшенных консолей с нагрузкой заменим на каждой опоре сосредоточенным моментом    и силой F. Реакция опор балки в этом случае будет равна F.

Граничные условия: , , , , , .

Тогда ;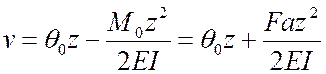

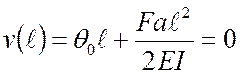; ; отсюда .

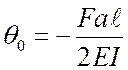Таким образом, ,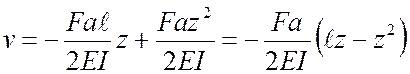

при 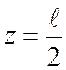; 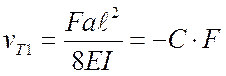, где .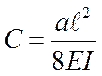

Подсчитав по исходным данным коэффициент С, можно заполнить таблицу результатов теоретических расчетов по приближенному дифференциальному уравнению.

Определение прогибов с помощью точного уравнения
изогнутой оси балки.

В данной частной задаче, учитывая условия чистого изгиба, можно без больших математических затруднений найти точное значение теоретических прогибов в исследуемой балке . Для этого воспользуемся зависимостью (11.1) из  предыдущей лабораторной работы:

.

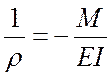 Так как  по всей длине балки, приходим к выводу, что балка изгибается по окружности радиусом : 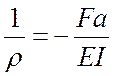. Тогда из рис.12.4 нетрудно найти

;

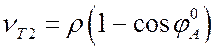где ; .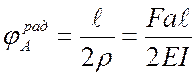

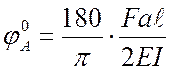Значения  при различных значениях F так же записываются в таблицу.

Рис. 12.4

По данным сводной таблицы строятся графики изменения , ,  в функции от F.

Выводы: на основе анализа графиков и данных сводной таблицы необходимо дать оценку возможности применения приближенного дифференциального уравнения изогнутой оси применительно к балкам исследованной и большей жесткости во всем диапазоне упругих деформаций.

Контрольные вопросы.

1.  Какая схема загружения осуществлялась при выполнении опыта?

2.  С чем связана установка жестких консолей за пределами опор?

3.  Каково отношение высоты балки к ее пролету ?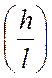

4.  Какой метод применялся для теоретического определения прогибов в исследуемом сечении балки?

Лабораторная работа № 13.

ИЗГИБ ЛИСТОВОЙ РЕССОРЫ

Цель работы: оценить точность определения прогибов в рессоре с помощью приближенного дифференциального уравнения изогнутой оси.

Рессора – это балка переменной жесткости. Она значительно более гибкая, чем равнопрочная ей балка постоянной по длине жесткости. Именно по этой причине рессора применяется для смягчения динамических воздействий (толчков, ударов), передаваемых через нее.

Рис. 13.1

Рессора является балкой равного сопротивления, во всех ее поперечных сечениях наибольшие нормальные напряжения остаются одинаковыми

.

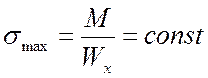Такой эффект  достигается тем, что одновременно с изменением изгибающего момента (рис.13.1,б) по длине балки меняется и ширина поперечного сечения (рис.13.1,в):

.

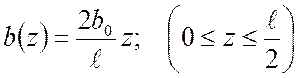Толщина листа рессоры . Учитывая это,

,

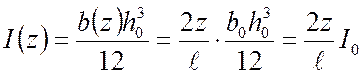где 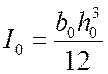 - момент инерции прямоугольного сечения относительно нейтральной оси в середине балки при .

Однако рессору было бы неудобно делать в виде ромбовидной в плане полосы (рис.13.1, в), поэтому этот ромб рассекают на продольные полосы, которые складывают друг друга и скрепляют хомутом (рис.13.1, г). Если пренебречь силами трения между листами, то можно считать, что эта конструкция работает на изгиб так же, как и ромб, изображенный на рис.13.1, в.

Таким образом, при расчете прогиба рессоры в середине пролета с помощью приближенного дифференциального уравнения изогнутой оси не учитываются не только те факторы, которые перечислены в лабораторной работе № 11, но еще и силы трения между листами рессоры.

Постановка и проведение опыта

Для выполнения опыта на прессе устанавливается рессора. Нагрузка прикладывается к середине пролета и в этом же сечении, внизу, устанавливается индикатор часового типа для измерения прогибов рессоры. После этого для обжатия рессоры прикладывается начальная нагрузка F₀, берется начальный отсчет по индикатору, затем нагрузка увеличивается одной или двумя ступенями, берутся новые отсчеты по индикатору и определяется прогиб рессоры - .

Теоретическое определение прогиба рессоры

Определить прогибы в рессоре по методу начальных параметров нельзя, так как этот метод пригоден только при . Поэтому используем прямое интегрирование приближенного дифференциального уравнения изогнутой оси балки , где функцией от  являются не только изгибающий момент  и прогиб , но и момент инерции :

;       .

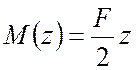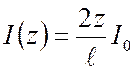Тогда

.

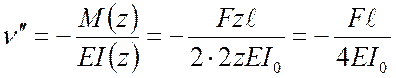Интегрируя это выражение, получим

,

.

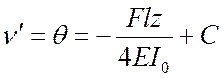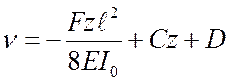Граничные условия:

-  при ; ;

-  при ; .

Из первого граничного условия находим ; из второго – найдем .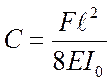

Следовательно,

.

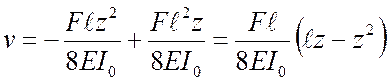Отсюда

при , .

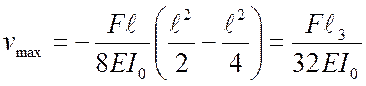По этой зависимости и подсчитывается теоретическое значение прогиба рессоры.

Равнопрочная с рессорой балка постоянной жесткости должна была бы по всей длине сохранить постоянную ширину . Можно подсчитать (это предлагается студентам проделать самостоятельно), что в этом  случае

.

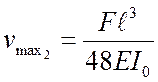Таким образом, убеждаемся, что прогиб в рессоре в 1,5 раза больше, чем в равнопрочной балке постоянного по длине сечения.

Выводы: сравнивая значения прогиба рессоры, найденные опытным и теоретическим путем, нужно дать оценку допущениям, положенным в основу теоретическим зависимостям.

Контрольные вопросы.

1.  Почему рессору называют балкой равного сопротивления?

2.  Какой метод применялся при расчете прогиба рессоры в середине пролета?

3.  По какой формуле подсчитывался осевой момент инерции сечения ?

4.  Проведите сравнение прогибов, найденных теоретически для рессоры и равнопрочной ей балки постоянной по длине жесткости.