Методические рекомендации к выполнению лабораторных работ по дисциплине "Сопротивление материалов". Часть 1, страница 8

выведенной при изучении теории чистого сдвига. Эта формула примечательна тем, что связывает все упругие постоянные материала - модуль Юнга Е, модуль сдвига Gи коэффициент Пуассона .

В выводах необходимо отразить, справедлив ли закон Гука при кручении. Сравнить значения модуля упругости, найденные опытным путем и теоретически.

Контрольные вопросы:

1.  Напишите выражение для закона Гука при чистом сдвиге. Поясните входящие в него величины.

2.  Напишите выражение для модуля сдвига через модуль продольной упругости и коэффициент Пуассона.

3.  Что характеризует собой модуль сдвига? В каких единицах он измеряется?

4.  Какую деформацию стержня называют кручением?

5.  Какую деформацию испытывает материал вала при чистом кручении?

6.  Что называется жесткостью вала при кручении?

Лабораторная работа № 7

ИСПЫТАНИЕ СТАЛЬНОГО ОБРАЗЦА НА ПЕРЕРЕЗЫВАНИЕ

Цель работы: определение предела прочности стали на срез и сравнение его с пределом прочности на разрыв.

В опыте испытывается стальной образец круглого поперечного сечения, изготовленный из малоуглеродистой стали.

Перед испытанием образец измеряется и закладывается в приспособление, изображенное на рис. 7.1. Принцип действия приспособления понятен из рисунка.

Рис. 7.1

Нагрузка растет статически до максимальной величины  (разрушающая нагрузка), которая фиксируется на шкале динамометра машины.

Определив разрушающую силу и зная площадь среза , равную удвоенной площади поперечного сечения образца, можно подсчитать предел прочности на срез по формуле

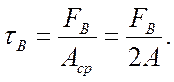                                                  (7.1)

Предел прочности на разрыв определяется косвенным путем посредством числа твердости по Бринеллю () по эмпирическому соотношению для малоуглеродистой стали

                                             (7.2)

Для определения числа твердости  перед испытанием на срез на торце образца делается лунка с помощью пресса Бринеля (см. лабораторную работу № 2).

Определив предел прочности на срез и на разрыв, можно найти их отношение

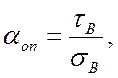                                                          (7,3)

Результаты опыта.

Полученные из опыта пределы прочности стали при срезе и разрыве отличны по величине, а отношение (7.3) для данного материала достаточно стабильно (если испытать серию образцов).

Величина коэффициента α может быть определена и теоретически по формуле

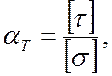                                                          (7.4)

где

·   - -допускаемое касательное напряжение;

·   - допускаемое нормальное напряжение.

В соответствии с энергетической теорией прочности, применительно к состоянию чистого сдвига,

,

Очевидно, величина  окажется больше . Одной из причин тому является наличие остаточных деформаций при определении , что вызывает перераспределение напряжений, тогда как  определяется исходя из условия, что элемент объема деформируется упруго.

В выводах нужно сформулировать понятие о напряженном состоянии чистого сдвига, указать, какие виды деформаций возникают вблизи места среза образца, объяснить причины различия в величинах коэффициентов  и .

Контрольные вопросы:

1.  Как определялась на опыте и чему равна величина предела прочности при срезе?

2.  Как в данном опыте был найден предел прочности при растяжении  испытываемого стального образца ?

3.  Каково соотношение между пределами прочности на срез и на разрыв  и можно ли его сравнить с соотношениями , получаемыми в теориях прочности и пластичности? 

Лабораторная работа № 8.

ОПРЕДЕЛЕНИЕ ДЕФОРМАЦИИ ВИНТОВОЙ ПРУЖИНЫ

Цель рабты: экспериментальная проверка формулы для определения деформации винтовой пружины с малым шагом витков.

Постановка эксперимента.

Схема установки изображена на рис.8.1

Рис. 8.1

На опорную плиту  (с отверстием), закрепленную на станине, ставится пружина. На пружине размещается диск, тоже c отверстием. Через пружину и отверстия в плите и диске пропускается стержень  с крюком на одном конце и нарезкой для несквозной гайки  на другом. На верхний конец стержня навинчивается гайка, через которую (посредством диска, стержня и поддона ) к пружине прикладывается нагрузка. Она равна весу гирь, положенных на поддон, и весу системы, через которую груз действует на пружину.

Для измерения осадки пружины применяется индикатор – прибор, предназначенный для измерения линейных перемещений. Он закрепляется на станине с помощью специального штатива и располагается так, чтобы шток индикатора опирался на плоский торец несквозной гайки. Этим прибором можно измерить перемещение в пределах от 0 до 10 мм.

Проведение эксперимента

До начала загружения, штангенциркулем измеряется (с точностью до 0,1 мм) наружный диаметр  Dпружины и диаметр стержня d, из которого она изготовлена.

Кроме геометрических размеров пружины, нужно знать число витков n и модуль сдвига G.

Опыт начинают с загружения пружины небольшой нагрузкой, которая могла бы ликвидировать зазоры между соприкасающимися поверхностями. Если в опыте используется установка, изображенная на рис.8.1,  то начальной нагрузкой F₀ может быть груз, равный весу системы (гайки, диска, стержня, поддона). При этой нагрузке берется первый отсчет по индикатору. Далее груз на поддоне увеличивают равными ступенями .

Такое нагружение позволяет проверить на опыте справедливость закона Гука для пружины.

Примерно одинаковая величина осадки  пружины от равных приращений нагрузки на величину , говорит о том, что между  и  наблюдается линейная зависимость, т.е. опытом подтверждается справедливость закона Гука. Величина осадки пружины λ от приращения нагрузки на , может быть вычислена теоретически по формуле:

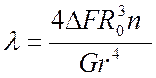                                                  (8.1)

где

·   – приращение нагрузки на пружину;

·  R₀ – расчетный радиус пружины, равный      ;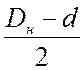

·  n– число витков;

·  G – модуль упругости при сдвиге;

·  r – радиус сечения стержня.