Методические рекомендации к выполнению лабораторных работ по дисциплине "Сопротивление материалов". Часть 1, страница 3

Числом твердости по Бринелю  называется отношение

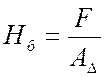
где   – площадь образовавшейся лунки,

.

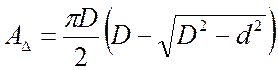Рис. 2.1

Между числом твердости по Бринелю  и временным сопротивлением при разрыве образца из пластичной стали существует соотношение

 (МПа).

Испытания проводятся на прессе Бринеля с механическим приводом. Основными характеристиками пресса при  проведении испытания являются диаметр шарика D, наибольшая нагрузка на шарик ,  время выдержки нагрузки t.

Диаметр отпечатка измеряется специальным микроскопом в двух взаимно перпендикулярных направлениях, из которых берется среднее значение. Зная диаметр отпечатка, диаметр шарика и нагрузку, по специальным таблицам (таблица 2), можно найти соответствующее этим данным число твердости по Бринелю.

Вывод: подсчитав по числу твердости временное сопротивление стали, можно сравнить его со значением временного сопротивления, полученным при непосредственном разрыве этого же образца.

Контрольные вопросы:

1.  Что такое «твердость материала»?

2.  Что называют числом твердости по Бринелю?

3.  Какова методика проведения опыта?

4.  Какая из механических характеристик прочности стали связана с числом твердости по Бринелю?

5.  В чем преимущество оценки прочности материала по числу твердости, по сравнению с испытанием на разрыв?

Таблица 2.

Определение числа твердости по Бринелю

Диаметр* отпечатка  или , мм	Число твердости по Бринелю, МПа, при нагрузке F, Н, равной
	300D2	100D2	25D2
2,90 2,95 3,00	4440 4290 4150	- - -	- - 346
3,05 3,10 3,15 3,20 3,25 3,30 3,35 6,40 3,45 3,50	4010 3880 3750 3630 3520 3410 3310 3210 3110 3020	- 1290 1250 1210 1170 1140 1100 1070 1040 1010	334 323 313      30,3 293 284 276 267 259 252
3,55 3,60 3,65 3,70 3,75 3,80 3,85 3,90 3,95 4,00	2930 2850 2770 2690 2620 2550 2480 2410 2350 2290	977 950 923 897 872 849 826 804 783 763	245 237 231 224 218 212 207 201 196 191
4,10 4,20 4,30 4,40 4,50	2170 2070 1970 1870 1790	724 688 655 624 595	181 172 164 156 149
4,60 4,70 4,80 4,90 5,00	1700 1630 1560 1490 1430	568 543 519 496 475	142 136 130 124 119

D=10мм. Для определения по таблице числа твердости при испытании шариком в 2,5 мм надо умножить на 4.

Лабораторная работа №3

ИССЛЕДОВАНИЕ ПРОЧНОСТНЫХ И ПЛАСТИЧЕСКИХ СВОЙСТВ МАТЕРИАЛОВ ПРИ СЖАТИИ

Цель опытов: сравнительное изучение свойств различных материалов при испытании их на статическое сжатие.

Испытанию на сжатие подвергаются образцы пластичной стали, чугуна, дерева, цементного камня. Образцы древесины, как материала анизотропного, испытываются вдоль, и поперек волокон.

Вид образцов для испытания на сжатие влияет на величины определяемых механических характеристик, поэтому их делают стандартных размеров и формы в соответствии с требованиями ГОСТа.

Испытания проводят на гидравлическом прессе. Пресс имеет устройство для автоматического вычерчивания диаграмм сжатия. Приспособление дает диаграммы малого размера и небольшой точности. Поэтому эти диаграммы обычно используются лишь для качественной иллюстрации процесса сжатия, но не для количественных измерений.

3.1 Исследование на сжатие образца из пластичной стали.

Образец изготавливается в форме цилиндра, высота которого удовлетворяет требованиям: . Перед испытанием измеряется высота – с точностью до 0,1 мм и диаметр – до 0,01 мм.

В процессе сжатия образец расширяется, принимая бочкообразную форму, и даже расплющивается без видимых признаков разрушения (рис. 3.1). В случае недостаточной пластичности материала на боковой поверхности образца могут появиться мелкие трещины, не ведущие, однако, к полному разрушению. Опыты приходится прекратить, не определив разрушающей нагрузки. Примерный вид диаграммы сжатия, получающейся при этом испытании, представлен на рис. 3.2. На диаграмме хорошо заметен участок упругого деформирования образца в соответствии с законом Гука. Можно найти нагрузку  и подсчитать предел пропорциональности стали , поделив  на первоначальную площадь сечения образца.

Однако обнаружить площадку текучести, подсчитать предел текучести, временное сопротивление в данном опыте невозможно. Объясняется это тем, что при сжатии образца за пределом пропорциональности происходит постоянное увеличение поперечного сечения, поэтому даже для поддержания постоянного напряжения нагрузка все равно должна расти. На участке же упрочнения рост деформаций, как это было показано на примере диаграммы растяжения, сопровождается ростом напряжений, поэтому при сжатии, вызывающем значительное расширение образца, нагрузка на него растет особенно интенсивно и со все возрастающей скоростью.

Рис. 3.1                                                    Рис. 3.2

3.2 Исследование на сжатие образца из чугуна.

Образец имеет форму цилиндра с размерами . Высота измеряется с точностью до 0,1 мм, диаметр – до 0,01 мм.

В процессе сжатия образец приобретает бочкообразную форму, что свидетельствует о небольших пластических деформациях, а затем внезапно разрушается, о чем можно судить по резкому падению нагрузки. На боковой поверхности образца появляются трещины, ориентированные приблизительно под углом  (рис. 3.3).

Рис. 3.3                                                       Рис. 3.4

Диаграмма сжатия чугуна (рис. 3.4) имеет вид, характерный для хрупких материалов. Протяженность ее вдоль оси  мала; единственная из механических характеристик прочности, которую можно в данном случае найти, - это предел прочности .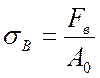

3.3 Исследование на сжатие дерева вдоль и поперек волокон