Методические рекомендации к выполнению лабораторных работ по дисциплине "Сопротивление материалов". Часть 1, страница 5

При растяжении или сжатии образца деформации происходят не только в продольном направлении, но и в поперечном. Опытным путем установлено, что соотношение между относительными поперечными  и относительными продольными  деформациями в пределах пропорциональности  есть величина постоянная для каждого материала:

.

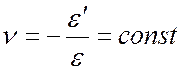Эта величина называется коэффициентом Пуассона. Знак минус в этой зависимости объясняется тем, что деформации  и  всегда противоположны по знаку. Например, при растяжении продольная деформация (удлинение) положительна, а поперечная (сжатие) – отрицательна.

        Итак, модуль продольной упругости и коэффициент Пуассона – это постоянные, характеризующие упругие свойства материала.

Для определения упругих постоянных стальной образец подвергается растяжению и проводится измерение упругих деформаций в продольном и поперечном направлениях.

Измерение линейных упругих деформаций производится с помощью рычажных тензометров. Схема прибора показана на рис.4.1.

Рис. 4.1

Прибор крепится к образцу С. Расстояние между нижним ребром подвижной призмы  и острием неподвижного ножа называется базой прибора. Рычаг жестко соединен с опорной призмой и шарнирно связан тягой с показывающей стрелкой, один конец которой закреплен неподвижно, а другой перемещается по зеркальной шкале.

При изменении длины образца на базе  на величину  произойдет поворот призмы , и соединенный с ней рычаг с помощью тяги  переместит стрелку на величину . Разность отсчетов  пропорциональна удлинению . Коэффициент увеличения прибора К измеряется соотношением плеч в рычажной системе прибора и равен

.

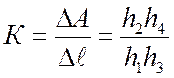Обычно К=900÷1200. Зная коэффициент увеличения прибора К, можно найти деформацию .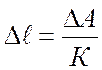

Таким образом, характеристиками тензометра являются база прибора  и коэффициент увеличения К.

С учетом удобства размещения измерительных приборов, экспериментальный образец изготовлен в форме сравнительно тонкой, но достаточно широкой и длинной пластины (рис.4.2).

Ее поперечные размеры должны быть измерены перед испытанием с точностью до 0,1 мм. Тензометры для измерения продольных и поперечных деформаций устанавливаются попарно с противоположных сторон образца – пластины. Такое размещение тензометров позволяет, во-первых, обнаружить неточности центрирования образца и, по возможности, их устранить; а, во-вторых, привести показания приборов к оси образца и, таким образом, исключить ошибку в показаниях, связанную с эксцентриситетом приложения нагрузки.

Рис. 4.2

Методика проведения опыта

Чтобы проверить справедливость закона Гука в условиях осевого растяжения, необходимо убедится в существовании линейной зависимости упругих продольных и поперечных деформаций от нагрузки, приложенной к образцу. Поэтому нагружение будем проводить равными ступенями. Число ступеней должно быть не слишком мало, так как иначе трудно сделать надежный вывод о закономерности, связывающей  и F. Оптимальное число ступеней нагрузки .

Обработка результатов опытов

Прежде всего необходимо проанализировать полученную в опыте зависимость между нагрузкой F и деформациями образца. Проще всего, а главное нагляднее, это можно сделать, построив по экспериментальным данным график . Абсолютное значение продольной деформации образца от изменения нагрузки на  равно приращению показаний по двум тензометрам, деленному на два и на коэффициент увеличения:

.

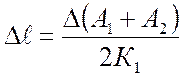При этом относительная продольная деформация от одной ступени нагрузки равна .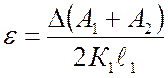

Абсолютное значение продольной деформации, после п ступеней нагрузки, равно:

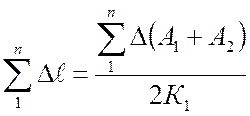
а относительная деформация

,

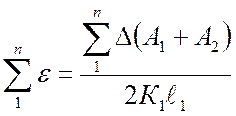где К₁ и  - коэффициент увеличения и база тензометров, измеряющих продольную деформацию.

Для абсолютных и относительных значений поперечных деформаций получаем аналогичные зависимости:

-  от одной ступени нагрузки

, ;

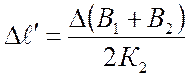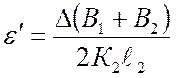-  от п ступеней нагрузки

, ,

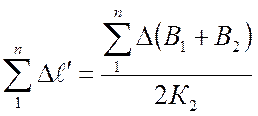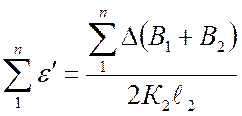где К₂ и  - коэффициент увеличения и база тензометров, измеряющих поперечные деформации.

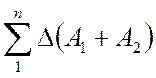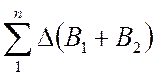Таким образом, продольные и поперечные деформации в процессе опыта пропорциональны величинам  и  соответственно. По данным опыта построим экспериментальный график, выражающий зависимость между F и 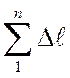, причем  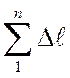будет увеличено в 2К раз (рис. 4.3).

Рис. 4.3

Если экспериментальные точки на графиках хорошо согласуются с прямолинейными зависимостями, можно сделать вывод о том, что закон Гука как для продольных, так и для поперечных деформаций справедлив.

В таком случае  для подсчета модуля упругости можно воспользоваться законом Гука в форме

,

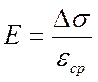где  - приращение напряжения на одной ступени нагрузки ,

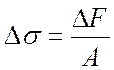 - среднее значение относительной продольной деформации от одной ступени нагрузки,

.

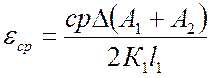Для подсчета коэффициента Пуассона найдем среднее значение относительной поперечной деформации от одной ступени нагрузки

.

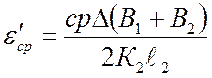Тогда коэффициент Пуассона

.

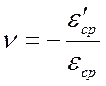Из наблюдения, что график  для продольных и поперечных деформаций может быть интерпретирован двумя пересекающимися прямыми, следует заключение о постоянстве коэффициента Пуассона в пределах пропорциональности.

В выводах необходимо дать оценку, подтверждается ли в проведенном опыте закон Гука для продольных и поперечных деформаций, постоянен ли коэффициент Пуассона в пределах пропорциональности. В заключении рекомендуется сопоставить опытные значения Е и  с табличными.

Контрольные вопросы.

1.  Какие упругие постоянные определяются в этом опыте? Дайте их определение.

2.  Почему для измерения продольных и поперечных деформаций  устанавливаются по два рычажных тензометра?

3.  Почему методика опыта предусматривает не однократное, а ступенчатое нагружение исследуемого образца?

4.  Чем можно подтвердить, что в процессе испытания имеют место только упругие деформации и что закон Гука не нарушался?

5.  Как при обработке результатов подсчитывался модуль продольной упругости Е и коэффициент Пуассона?

Лабораторная работа №5.

ИССЛЕДОВАНИЕ ОСОБЕННОСТЕЙ НАПРЯЖЕННОГО СОСТОЯНИЯ ПОЛЯРИЗАЦИОННО-ОПТИЧЕСКИМ МЕТОДОМ