Опыт проводится на консольной балке, сечение которой представляет собой швеллер. На свободном конце швеллера имеется приспособление, позволяющее перемещать положение точки приложения внешней нагрузки по горизонтали, и другое приспособление, позволяющее обнаружить появление поворота торцевого, свободного сечения балки в случае возникновения кручения. Приспособление для загружения (рис.10.2) представляет собой планку с мерной линейкой, жестко закрепленную на свободном конце швеллера перпендикулярно к его стенке. Параллельно планке по стержню скользит ползунок с поддоном для установки грузов. С помощью стрелки на ползунке по мерной линейке можно отмечать положение точки приложения груза по отношению к стенке швеллера.
|
|
|
|
а) |
б) |
|
Рис. 10.2 |
|
Для выявления поворота поперечного сечения свободного конца швеллера относительно продольной оси стержня используется следующее приспособление. Это два индикатора, закрепленные на станине установки (рис.10.2,а). Ножки индикаторов упираются в опорные площадки на консолях, жестко соединенных со стенкой свободного конца швеллера. О повороте сечения швеллера можно судить по разности между показаниями левого и правого индикаторов.
Если разность показаний правого больше, чем левого, то имеет место поворот по часовой стрелке. Если разность показаний левого индикатора больше, чем правого, то сечение поворачивается против часовой стрелки. Если разности показаний слева и справа одинаковы, то это означает, что поворота сечения нет.
Проведение опыта
Сначала расположим поддон для грузов так, чтобы он находился на вертикали центра тяжести сечения швеллера, и начинаем загружение. наблюдая при этом за поворотами поперечного сечения швеллера относительно оси стержня. В ходе опыта наблюдается заметный поворот сечения. Следовательно, когда нагрузку приложим в центре тяжести, то происходит и изгиб стержня, и его закручивание.
После этого начнем смещать ползунок (рис.10.2) во внешнюю сторону от стенки швеллера и повторять загружение до тех пор, пока разности показаний правого и левого индикаторов не будут одинаковы. При этом точка приложения нагрузки будет соответствовать положению центра изгиба, и по мерной линейке (рис.10.2) можно найти опытное значение величины хА - расстояние от оси стенки швеллера до центра изгиба.
Теоретические расчеты
По известным геометрическим размерам швеллера и полученной в теории формуле рассчитывается теоретическое значение расстояния от центра изгиба до оси стенки швеллера
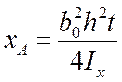
Необходимо сравнить значения xA, найденные экспериментально и теоретически, оценить расхождение между ними в процентах.
В выводах надо не только отметить степень согласования между экспериментальными и теоретическими значениями хА , но и указать, как необходимо прикладывать нагрузку к несимметричным тонкостенным профилям, чтобы в них происходил только плоский изгиб и исключалось кручение.
1. Что такое центр изгиба сечения балки?
2. Как должна прикладываться нагрузка к балке с поперечным сечением, представляющим собой незамкнутый тонкостенный профиль?
3. Какой вид деформации будет испытывать стержень, если линия действия внешней нагрузки будет проходить через центр изгиба?
ИССЛЕДОВАНИЕ ГРАНИЦ ПРИМЕНИМОСТИ ПРИБЛИЖЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ИЗОГНУТОЙ ОСИ БАЛКИ
Цель работы: экспериментальная оценка границ применимости приближенного дифференциального уравнения изогнутой оси к балке сравнительно малой жесткости.
Исходные положения.
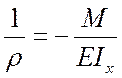 (11.1)
(11.1)
Вывод
производился для случая чистого изгиба, когда ![]() ,
кроме того были приняты гипотеза плоских сечений и гипотеза о том, что продольные
волокна не давят друг на друга.
,
кроме того были приняты гипотеза плоских сечений и гипотеза о том, что продольные
волокна не давят друг на друга.
Точное дифференциальное уравнение изогнутой оси балки можно записать
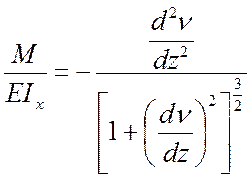 ,
(11.2)
,
(11.2)
в него заложены те же предпосылки, что и в (11.1).
Учитывая, что квадрат ![]() при относительно небольших
прогибах есть величина малая по сравнению с единицей, то пренебрегая ею,
получим приближенное дифференциальное уравнение изогнутой оси балки
при относительно небольших
прогибах есть величина малая по сравнению с единицей, то пренебрегая ею,
получим приближенное дифференциальное уравнение изогнутой оси балки
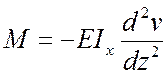 или
или ![]() (11.3)
(11.3)
Таким образом, уравнение (11.3) получено на основе ряда допущений. Среди них наиболее существенны два: пренебрежение влиянием на величину прогибов поперечной силы Q и наложение ограничений на величину определяемых прогибов. В настоящей работе нас интересуют именно последние ограничения.
Прежде чем перейти к
конкретным опытам, рассмотрим один важный в данном случае вопрос: как влияет
отношение ![]() на возможную величину наибольшего
относительного прогиба, т.е. на величину
на возможную величину наибольшего
относительного прогиба, т.е. на величину ![]() ?
?
При изгибе стержня возникают
напряжения и появляются перемещения, в частности прогибы. С увеличением
прогибов напряжения возрастают. При всех условиях прочность балки не должна
быть нарушена, а это означает, что должно выполняться условие ![]() , где
, где 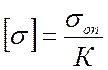 (
(![]() - опасное для материла напряжение, к
– коэффициент запаса прочности, к>1).
- опасное для материла напряжение, к
– коэффициент запаса прочности, к>1).
При изгибе, исходя из
гипотезы плоских сечений, имеем ![]() , т.е.
относительная деформация волокон балки возрастает с увеличением у – расстояния
от нейтрального слоя до волокна балки и с увеличением
, т.е.
относительная деформация волокон балки возрастает с увеличением у – расстояния
от нейтрального слоя до волокна балки и с увеличением ![]() -
кривизны стержня.
-
кривизны стержня.
Принимая гипотезу о том, что
волокна друг на друга не давят, получаем зависимость для ![]() в виде
в виде
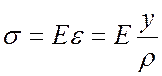 ,
,
при этом 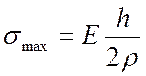 (для балки,
имеющей две оси симметрии в поперечном сечении). Учитывая, что
(для балки,
имеющей две оси симметрии в поперечном сечении). Учитывая, что ![]() , имеем
, имеем 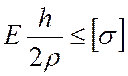 .
Значит, чем больше высота балки, тем меньше для нее предельно допускаемое значение
кривизны
.
Значит, чем больше высота балки, тем меньше для нее предельно допускаемое значение
кривизны ![]() , а, следовательно, и значения
, а, следовательно, и значения ![]() . Так как напряжения в балке зависят
от изгибающего момента, а он в свою очередь связан с размерами балки по длине,
значение
. Так как напряжения в балке зависят
от изгибающего момента, а он в свою очередь связан с размерами балки по длине,
значение ![]() при определенной кривизне стержня
при определенной кривизне стержня ![]() тоже зависит от длины стержня.
Высказанную выше мысль лучше сформулировать так: чем больше относительная
высота балки
тоже зависит от длины стержня.
Высказанную выше мысль лучше сформулировать так: чем больше относительная
высота балки ![]() , тем меньше для нее
допускаемое по условию прочности значение относительного прогиба
, тем меньше для нее
допускаемое по условию прочности значение относительного прогиба 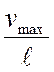 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.