









































Цель курса
Данный курс служит для развития навыков работы с формальными алгебраическими системами. Элементами таких алгебраических систем являются не числа, а некоторые объекты, являющиеся либо компонентами некоторой модели (в этом случае свойства рассматриваемых объектов отражают свойства некоторой предметной области, например, направленный граф может отражать структуру реального объекта) и служат для их исследования, либо искусственно "созданными" (первоначально только в виде модельного представления) объектами с заданными свойствами для последующей реализации по их подобию реальных технических устройств которые не могли бы быть заменены существовавшими объектами в виду отсутствия у них необходимых свойств. Последний случай особенно труден для понимания как раз в виду отсутствия аналогий с какими-либо первичными материальными (физическими) объектами, явлениями. Хотя такие "предметы", как электронные устройства передачи, хранения и обработки информации, уже рассматриваются как существующее окружение современного человека, и входит в его повседневный опыт, по существу они являются реализацией функций формальных моделей, первичных по отношению к ним, а не построенных для их исследования.
Представленные материалы следует рассматривать как сжатое изложение таких учебников, как [1]. Они могут оказаться полезными и при самостоятельном рассмотрении литературы по теории кодирования, например [2].
Литература:
1. Г. Биркгоф, Т. Барти. Современная прикладная алгебра. М.:Мир 1976
2. Т. Касами, Н. Токура, Е. Ивадари, Я. Иганаки. Теория кодирования. М.:Мир 1975.
Рассматриваемые в курсе объекты можно отнести к классам, определяемым на основе следующих основных понятий:
1. Множество
2. Элемент
3. Отношение принадлежности
4. Унификация объектов
5. Структурность объектов
Сами эти понятия, являясь первичными, не могут быть определены. К множествам можно отнести те объекты (скорее всего, абстрактные), которые выступают в роли объединяющих понятий, которым могут принадлежать другие объекты (любой природы: конкретные и абстрактные, возможно, даже множества) в качестве элементов. Само понятие отнесения объекта к классу также может быть представлено как принадлежность элемента к множеству.
Множество и элемент находятся в отношении принадлежности. Запись xÎA означает, что элемент x находится в отношении принадлежности к множеству A. Форма записи, когда символ, обозначающий отношение, расположен между соотносимыми символами, называется инфиксной. Ее можно рассматривать как бинарную операцию со значениями ИСТИНА и ЛОЖЬ. Под унификацией объектов понимается возможность установить, что различными символами обозначен один и тот же объект при рассмотрении выражений вида a=b. В последнем случае можно говорить об инфиксной записи для бинарной операции, принимающей значения ИСТИНА, если символы a и b обозначают один и тот же объект. Само высказывание один и тот же объект зависит от рассматриваемой предметной области и нуждается в определении или аксиоматическом задании.
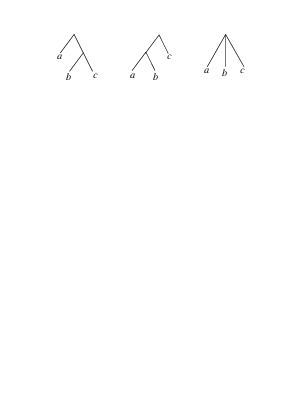
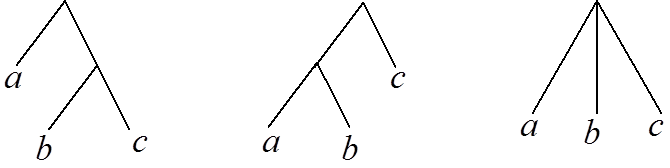
Понятие структурности объекта означает возможность унификации "по частям". Структурные части при записи перечисляются через запятую, а все перечисление заключается в скобки (обычно круглые). Запись x=(a,b) означает, что у объекта, обозначенного символом x, можно выделить часть, обозначенную символом a, и часть, обозначенную символом b. При этом взаимное расположение частей (порядок записи) важен. Аналогично происходит разделение на большее число частей, например x=(a,b,c). Наоборот, можно рассматривать символы, обозначающие структурность как конструкторы, позволяющие из существующих объектов создать новый. Применяя эту процедуру несколько раз, можно описать вложенную структуру, например, x=(a,(b,c)). Для унификации необходимо совпадение структур объектов и соответствующих структурных частей:
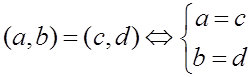
Поэтому (a,(b,c))¹((a,b),c) и (a,(b,c))¹(a,b,c).
Отличие между такими объектами можно представить графически:
Отношения между множествами
Отношение равенства между множествами определяется следующим образом:
A=BÛ(xÎAÛxÎB)
Отношение включения между множествами определяется следующим образом:
AÌBÛ(xÎAÞxÎB)
Следствие:
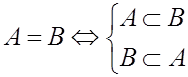
Задаются множества
1. Перечислением элементов. В этом случае проверка утверждения о принадлежности элемента множеству заключается в поиске элемента в списке:
A={x1,x2,¼,xn-1,xn}Þ(xÎAÛ$i:x=xi)
2. Заданием условия принадлежности элемента множеству.
A={x|P(x)}Þ(xÎAÛP(x))
Здесь P(x) - высказывание, принимающее значения ИСТИНА или ЛОЖЬ.
Свойства отношений равенства множеств и включения
Равенство
1. Рефлексивно: A=A
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.