Множества и операции над ними. Отношение принадлежности. Множество. Элемент. Унификация объектов, страница 11

Пример задания кода - двоичный групповой систематический (3,б) код:

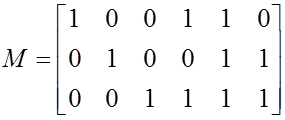
Схема кодирующего устройства приведена на рис. 6.

Рис. 6.

Чтобы сделать связь структуры кодера с порождающей матрицей нагляднее, схема умышленно оставлена неоптимальной по сложности (числу операций Å).

Рассмотрим теперь построение декодера и оценим его сложность. Всего из канала может быть получено 2ⁿ различных блоков. Если сопоставить каждому возможному входу выход декодера из k разрядов оценки  и еще один разряд - признак неисправимой ошибки, потребуется память из 2ⁿ (k+1)-разрядных ячеек. Декодирование осуществляется за одну операцию выборки из памяти. Такой подход пригоден только для очень малых размеров блоков.

Для упрощения декодирования рассмотрим разбиение множества A на смежные классы по подгруппе B: A/B={y+B|yÎA}. Смежный класс, порожденный нейтральным элементом - вектором 0 - запишем в виде первой строки таблицы, а остальные классы - следующими строками. Первая строка совпадает с самой подгруппой допустимых кодовых комбинаций 0+B=B. Всего в таблице будет 2^n-k строк по 2^k элементов в каждой строке.

Рассмотрим условие возникновения необнаруженной ошибки. Для этого необходимо, чтобы ỹÎB или y+e=z, zÎB. Тогда, так как в рассматриваемой группе каждый элемент обратный самому себе, e=y+z и, так как yÎB, по замкнутости подгруппы относительно бинарной операции + eÎB. Таким образом, не обнаруживаются те и только те комбинации ошибок, векторные представления которых сами являются допустимыми кодовыми комбинациями. Всего таких комбинаций будет 2^k-1, так как элемент 0ÎB - не ошибка. Запишем первую строку таблицы так, чтобы первым элементом был вектор 0.

Остальные строки таблицы могут быть двух видов:

1) В строке (классе разбиения p+B) существует единственный элемент с наименьшим весом: $zÎp+B: "tÎp+B w(z)£w(t). Тогда такой вектор z назовем лидером класса p+B, выберем его порождающим элементом (любой элемент класса может быть порождающим) и запишем первым в данной строке.

2) В строке такого элемента нет - порождающим элементом выберем произвольный элемент класса и запишем первым в данной строке.

Порядок расположения остальных элементов в строках зададим такой, чтобы элемент являлся “суммой” (результатом бинарной операции +) между заголовком строки (лидером z для строк первого типа или произвольным порождающим элементом для строк второго типа) и заголовком столбца (элементом подгруппы допустимых кодовых комбинаций. Схема построения такой таблицы показана на рис. 7.

Рис. 7

На этом рисунке m строк первого типа и 2^n-k-m строк второго типа. Всеми своими элементами таблица полностью покрывает множество векторов, которые могут быть получены из канала. Поэтому правило оптимального приема с исправлением ошибок будет заключаться в следующем:

1) Если принятый вектор попал в первую строку, то наиболее вероятно, что ошибок нет и =f^-1(ỹ) - то есть для систематического кода просто берутся информационные символы.

2) Если принятый вектор попал в одну из строк первого типа, то наиболее вероятно, что ошибка имеет конфигурацию лидера этой строки, а передаваемая информация - заголовок столбца, содержащего принятый вектор.

3) Если принятый вектор попал в одну из строк второго типа, то фиксируется обнаруженная, но не исправляемая ошибка.