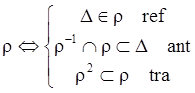
Используя св-ва операций над отношениями и св-ва степеней отн.
DÌrÞD-1Ìr-1ÞDÌr-1 ref (r-1)
r-1ÇrÌD ant (r-1)
r2ÌrÞ(r2)-1Ìr-1Þ(r-1)2Ìr-1 tra (r-1)
Þ теор: r - порядок Þ r-1.
r-1 называется порядком, двойственным к r
Пример: ³ и £ на R
m | n m делит n
m делится на n
Еще один важный пример:
Отношение включения на множестве всех подмножеств (частичный порядок)
U = P({1, 2, 3}) = {Æ, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}
Опр. Отрезок на частично-упорядоченном множестве А с порядком r
1) [a, b]r = {x | (a, x)Îr, (x, b)Îr}
2) Отрезок называется простым, если он содержит только свои границы:
[a, b]r = {a, b}
Пример: Отношение m делит n на N m|n:
[2, 8]1 = {2, 4, 8}
[3, 11]1 = Æ
[4, 8]1 = {4, 8}
2|2, 2|8; 2|4, 4|8; 2|8, 8|8
4|4, 4|8; 4|8, 8|8
Диаграмма Хассе: граф, в котором вершины соотв. элементам частично упорядоченного множества, причем
1) если (x, y)Îr, то y отображается выше x
2) 2 вершины соединяются между собой, если они явл. границами простого отрезка. (Петли тоже простые отрезки, но их не отображают)
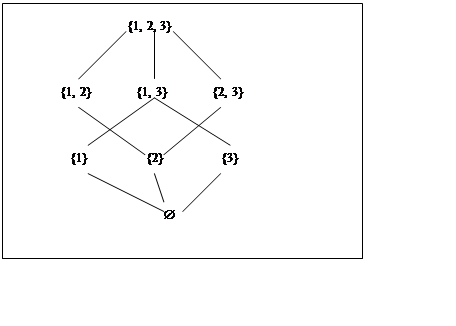 ÆÌ{1}, ÆÌ{2}, ÆÌ{3}
ÆÌ{1}, ÆÌ{2}, ÆÌ{3}
([Æ, {1, 2}])Ì =
={Æ, {1}, {2}, {1, 2}} –
не явл. простым)
Перевернуть, чтобы получить двойственный порядок É
¨ Упражнение
Построить диаграмму Хассе для отношения делимости чисел от 1 до 20.
Экстремальные элементы подмножеств частично упорядоченных множеств.
p - порядок. Исп. запись xpyÛ(x, y)Îp
<A, p> - частично упорядоченное множество XÌA
Опр.
1) аÎХ, наименьший элемент Х в смысле порядка p, если а p х "хÎХ; lt, Lt(X) – множество наименьших элементов.
2) аÎХ минимальный элемент Х в смысле порядка p, если хÎХ, хpа Þ х=а; min, Min(X) – мн-во минимальных элементов.
3) аÎХ называется нижней гранью Х в смысле порядка p, если а p х "хÎХ; inf
1)* 2)* 3)* Двойстренные: наибольший – gt, максимальный – max, верхняя грань – sup
4) X*={aÎA| a px "xÎX} – мн-во нихних граней
4)* X*={aÎA| x pa "xÎX} – мн-во верхних граней
5) Наибольший эл. Х* называется точной нижней гранью
5)* Наименьший эл. Х* называется точной верхней гранью
¨ Упражнение
1. Доказать, что наименьший элемент, если он существует, то он единственный.
2. Сколько различных отношений порядка можно построить на множестве из трех элементов. Привести все их диаграммы.
Замыкание отношений
rÌА2
Задача: наименьшим по числу добавляемых элементов (пар, стрелок) дополнить заданное отношение так, чтобы результат был
1. Рефлексивен
2. Симметричен
3. Транзитивен
Например, если требуется восстановить отношение порядка по его диаграмме Хассе, то транзитивное замыкание вместе с петлями будет решением.
I.
- рефл. замыкание r, если 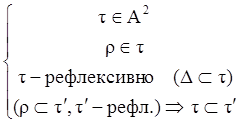
II.
- Симметричное замыкание r, если 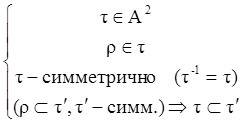
III.
- Транзитивное замыкание r, если 
Теор
1. t=rÈD - Рефл. зам. r
2. t=rÈr-1 – Симм. зам. r
3.
Если |A| = n Þ t=![]() =rÈr2È…Èrn – Транз. замыкание r
=rÈr2È…Èrn – Транз. замыкание r
Док-во:
1. t=rÈDÞ![]()
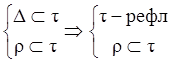
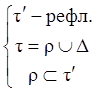 Þt=rÈDÌt¢ÈD=t¢, т.е. tÌt¢
Þt=rÈDÌt¢ÈD=t¢, т.е. tÌt¢
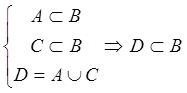
2. t=rÈr-1Þt -1=(rÈr-1)-1=r-1È(r-1)-1=r-1Èr=t, т.е. t -1=t, rÌt
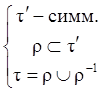 ÞrÌt¢Þr-1Ì(t¢)-1Þt=rÈr-1Ìt¢È(t¢)-1=t¢Èt¢=t¢, т.е. tÌt¢
ÞrÌt¢Þr-1Ì(t¢)-1Þt=rÈr-1Ìt¢È(t¢)-1=t¢Èt¢=t¢, т.е. tÌt¢
![]()
Для док-ва 3 сначала докажем:
(а) rÌtÞ rmÌtm, mÎN
База индукции rÌt
Индукц. предположение rmÌtm
rmÌtmÞtm=tmÈrm; rÌtÞt=tÈr
tm+1=tm°t=(tmÈrm)°(tÈr)=[tm°(tÈr)]È[rm°(tÈr)]= =(tm°t)È(tm°r)È(rm°t)È(rm°r)=rm+1ÈsÞrm+1Ìtm+1
(б) d2ÌdÞdkÌd "kÎN
База индукции: dÌd
Индукционное предположение: dкÌd
dk+1=dk°dÌd°d=d2ÌdÞdk+1Ìd, Ì - транз.
(в)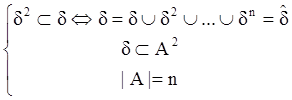
Þ : 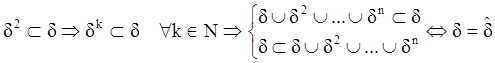
Ü : d=dÈd2È…ÈdnÞ![]()
= (Исп. дистрибутивность ° и È и св-ва степени отношения) =d2Èd3È…Èd2n
dqÌdÈd2È…Èd=![]() "qÎN по св-ву степ. отн. на кон.
мн-ве.
"qÎN по св-ву степ. отн. на кон.
мн-ве.
Þd2 Ì ![]() = dÈdÈ…Èd = d Þ d2 Ì d
= dÈdÈ…Èd = d Þ d2 Ì d
Док-во3:
t = rÈr2È…Èrn = ![]()
t2 = (rÈr2È…Èrn)![]() (rÈr2È…Èrn) = r2Èr3È…Èr2n Ì rÈr2È…Èrn = t
(rÈr2È…Èrn) = r2Èr3È…Èr2n Ì rÈr2È…Èrn = t
т.е. t2 Ì t Þ t - транз.
r Ì t
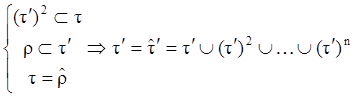
rÌt¢, r2Ì(t¢)2, … , rnÌ(t¢)n Þ
tÌrÈr2È…Èrn Ì t¢È(t¢)2È…È(t¢)n=![]() =t¢ÞtÌt¢
=t¢ÞtÌt¢
¨ Упражнение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.