Множества и операции над ними. Отношение принадлежности. Множество. Элемент. Унификация объектов, страница 5

1.  Восстановить отношение включения на подмножествах трехэлементного множества, воспользовавшись диаграммой Хассе. Сколько этапов необходимо?

2.  Докажите, что отношение порядка всегда можно восстановить по диаграмме Хассе.

(Рассмотрите отрезок между элементами, находящимися в отношении порядка и покажите, что можно построить цепь простых отрезков между такими элементами, если множество конечное)

9. Операции на множествах.

Опр.: n-местная (n-арная) операция на множестве A – любое функциональное отношение f из множества Aⁿ  в множество A.

Обозначение: , где f(x_1,…,x_n)=y.

Это частный случай (n+1) – арного отношения на А.

n=1 – унарная операция;

n=2 – бинарная

n=3 – тернарная

Набор из  называется алгебраической системой

 

множество операции отношения

Опр.: Набор из множества и операций называется Алгеброй.

Опр.: Набор из множества и отношений называется Математической моделью.

Опр.: Набор из множества и  f₁,…,f_m операций (n₁,…,n_m-арных) называется алгеброй типа (n₁,…,n_m).

Пример:  - алгебра типа (2, 2, 1)

Опр.:  - замкнуто относительно n-арной операции f на А, если

Опр.: ,  замкнуто относительно f₁,…,f_m Þ - подалгебра

Пример: ; R⁺ замкнуто относительно  - подалгебра

Бинарные операции на множестве:    

Опр.:  f – ассоциативна, если

 - ассоциативна

 - не ассоциативна  , т. к.

 - не ассоциативна 

Опр.: f – коммутативна, если

 - коммутативна

Рассмотрим две бинарные операции на А: f и y.

Опр.: f дистрибутивна относительно  y слева, если

Опр.: f дистрибутивна относительно  y справа, если

Опр.: f дистрибутивна относительно  y, если  f дистрибутивна относительно  y слева и f дистрибутивна относительно  y справа.

Инфиксная запись:

           Ассоциативность:  x  (y  z) = (x  y)   z

Коммутативность: x  y =  y  x

Дистрибутивность слева  относительно * :             x  (y*z) =  (x  y)*(x  z)

Дистрибутивность справа  относительно *:           (x*y) z =  (x  z)*(y  z)

Пример на R⁺:

· дистрибутивно слева и справа относительно + (или просто дистрибутивно)

+ не дистрибутивно слева и справа относительно ·

Опр.: Соотношением гомоморфизма между алгебрами одинакового типа и  называется любое функциональное отношение :

Опр.: Если F – биективно, то F – изоморфизм алгебр. (Взаимно однозначное соответствие).

Пример:  - изоморфизм

 - изоморфизм

Отношение изоморфизма (~) является отношением эквивалентности на множестве алгебр одинакового типа.

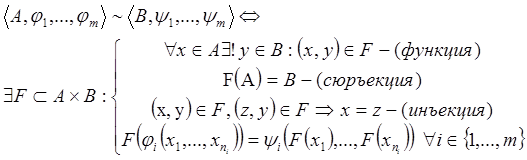
Чтобы показать, что ~ - эквивалентность, необходимо показать рефлексивность, симметричность и транзитивность:

1.  Рефлексивность:

6

2.  Симметричность:

Рассмотрим

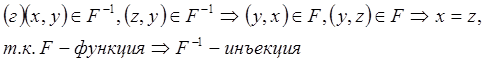
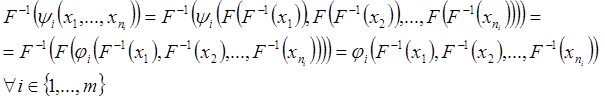
Т. е. если F – биекция из А в В, то F^-1 – биекция Þ F^-1 – изоморфизм Þ

3.  Транзитивность

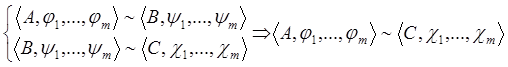
Пусть F – изоморфизм                                           F и G , т. к.

G – изоморфизм                                          

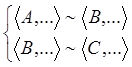
Рассмотрим отношение

Т. е. H – функция.

Т. к. H, G – биекции, то

 

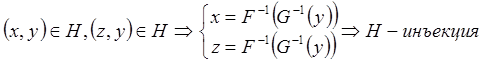
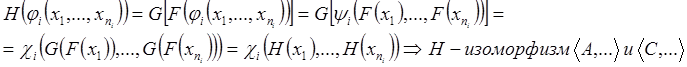
Пример:

т. к. F не биективна.

¨  Упражнение

Рассмотрите три алгебры

<R,+> - Сложение вещественных чисел

<R+,×> - Умножение вещественных положительных чисел

<R-,*> - Умножение отрицательных вещественных чисел с заменой знака: x*y=-(x×y).

Построить все шесть функций, являющихся изоморфизмами каждой пары алгебр с учетом их порядка в паре.

10. Бинарные алгебры (Алгебра с одной бинарной операцией).

Опр.:   Бинарная алгебра с ассоциативной операцией называется полугруппой (иногда называют группоидами).

Опр.: Элемент  называется левым нейтральным  элементом , если

Элемент  называется правым нейтральным  элементом , если

Элемент  называется  нейтральным  элементом , если

Опр.: Бинарная алгебра  называется моноидом, если

Свойство моноидов:

Т. е. в моноиде единственный нейтральный элемент.

Пример:  1.  - моноид с нейтральным элементом 0 (коммутативный).