Для
![]() (доопределяется степень элемента), т.е.
(доопределяется степень элемента), т.е.
![]() (По опр.)
(По опр.)
При этом ![]() , т.е.
Опр.:
, т.е.
Опр.: ![]()
Док-во: по индукции для ![]() по n, как и для степенного отношения.
по n, как и для степенного отношения.
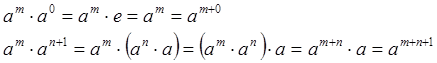
Если ![]() , то
, то
![]() - циклическая группа.
- циклическая группа.
Подгруппа: 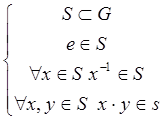 ,
т. е для S выполняются свойства замкнутости и свойства группы.
,
т. е для S выполняются свойства замкнутости и свойства группы.
Свойства степеней элемента:
Доопределим 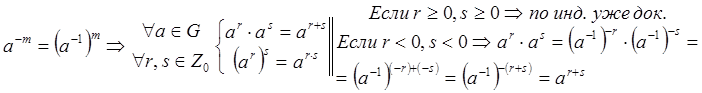
Если ![]()
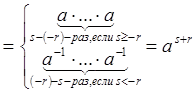
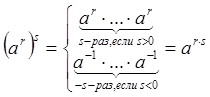
Следствие: В любой группе степени каждого элемента образуют подгруппу.
Пример:
![]() 8
8![]() - циклическая коммутативная группа.
- циклическая коммутативная группа.
![]()
![]()
1. Рассмотрим
произвольный моноид следующего вида ![]() (т. е.
(т. е. ![]() - ассоциативна,
- ассоциативна, ![]() )
)
![]() -
функциональное отношение:
-
функциональное отношение:
![]()
![]() -
образ А.
-
образ А.
![]()
Покажем, что ![]() :
:
![]() , т.
к.
, т.
к. ![]() .
.
Т. е. F(A) – замкнуто относительно ![]() .
.
![]() -
подмоноид моноида
-
подмоноид моноида ![]() .
.
![]()
![]() 6:
6:
![]() 6
6![]()
1). ![]() - функциональность:
- функциональность:
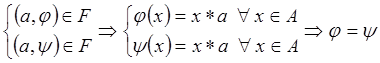
2). ![]() - инъективность
- инъективность
3). ![]() - соотношение гомоморфизма, т. к. F
инъективна и сюръективна
- соотношение гомоморфизма, т. к. F
инъективна и сюръективна ![]() ~
~![]() , т. е. Любой моноид
изоморфен некоторому моноиду преобразований на А.
, т. е. Любой моноид
изоморфен некоторому моноиду преобразований на А.
2. Теперь
будем считать, что ![]() - группа, · - ассоциативна
- группа, · - ассоциативна
![]()
![]()
Рассмотрим то же функциональное отношение:
![]() ,
, ![]()
F – биективно, F – гомоморфное наложение,
т. е. F – изоморфизм ![]() и
и ![]() .
.
В этом случае fa – биективно ![]()
![]()
=6![]() 6
6![]() 6
6![]()
6-
биективно ![]()
Если f – биективно, то f-1
– функционально и биективно, причем ![]() 6
6
Покажем, что ![]()
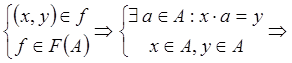
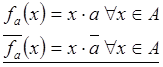
![]()
Преобразование на множестве А – любое
функциональное отношение, т. е. ![]() - множество всех
преобразований на А.
- множество всех
преобразований на А.
Система ![]() -
моноид; e = 6 (6 - функциональное отношение
– тоже функция), т. е. композиция функций есть функция;
-
моноид; e = 6 (6 - функциональное отношение
– тоже функция), т. е. композиция функций есть функция; ![]() -
ассоциативна (см. свойства
-
ассоциативна (см. свойства ![]() ).
).
6![]() 6
6
![]()
![]()
![]()
![]()
Пусть ![]() тогда
тогда![]() - подмоноид, если выполняются следующие
два условия
- подмоноид, если выполняются следующие
два условия
1. 6 ![]() ;
;
2. В
замкнуто относительно ![]() в
в ![]()
Рассмотрим произвольный моноид ![]() , в котором
, в котором ![]() -
ассоциативна и
-
ассоциативна и
![]() .
.
Покажем, что ![]() ~
~![]() , т. е.
, т. е. ![]()
![]()
1. ![]() - функциональность
- функциональность
2. ![]() - инъективность
- инъективность
3. ![]()
4. ![]() - соотношение гомоморфизма
- соотношение гомоморфизма
![]() Пусть
есть некоторая
Пусть
есть некоторая ![]()
Такая функция возможна, т. к. ![]()
![]() , т.
е. возможна биекция.
, т.
е. возможна биекция.
Возникает вопрос: как выбрать F, чтобы обеспечить замкнутость В?
Попробуем ответить на него: 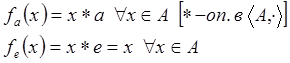
![]()
![]()
Покажем, что тогда ![]() :
:
![]()
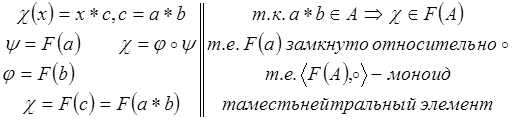
![]() 6.
6. ![]() -
ассоциативна.
-
ассоциативна. ![]()
F – инъективна: пусть ![]()
![]()
F – сюръективна (по определению В) т. е. ![]() ~
~![]() .
.
Подстановка – любое биективное функциональное отношение на А.
![]() -
группа, т. е.
-
группа, т. е.
· - ассоциативна;
e – нейтральный элемент: ![]() ;
;
![]()
![]()
Уже доказано, что F – биективно, F – гомоморфное наложение
Покажем теперь, что ![]() биективно
биективно ![]() :
:
![]() 6
6![]() имеет
место:
имеет
место:
![]() 6
6![]() 6
6![]()
6-
биективно ![]() .
.
Какой вид имеет ![]() ?
?
![]() .
.
Если f – биективно, то f-1 –
функционально и биективно, причем ![]() 6; а т. к. в
6; а т. к. в ![]() у каждого элемента единственный
обратный, то
у каждого элемента единственный
обратный, то ![]() .
.
Полезные сведения
Числа классов эквивалентности по изоморфизму в зависимости от числа элементов в группе:
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
# |
1 |
1 |
1 |
2 |
1 |
2 |
1 |
5 |
2 |
2 |
Обратите внимение, что группа простого порядка единственна с точностью до изоморфизма. Доказательства смотрите далее после рассмотрения теоремы Лагранжа.
¨ Упражнение
Используя свойство "каждый элемент в каждой строке и каждом столбце один и только один раз" (следствие сократимости), при фиксированном обозначении для нейтрального элемента получить все заполнения для таблицы групповой операции на четырехэлементном множестве и найти их изоморфизмы.
Например, выбрав во множестве {1,2,3,4} 1 как нейтральный элемент, таблица должна начинаться следующим образом:
|
* |
1 |
2 |
3 |
4 |
|
1 |
1 |
2 |
3 |
4 |
|
2 |
2 |
? |
? |
? |
|
3 |
3 |
? |
? |
? |
|
4 |
4 |
? |
? |
? |
Далее будем рассматривать группы:
![]()
Пусть![]() подгруппа
подгруппа![]() .
.
g – элемент G ![]()
Опр.:
![]() - левый смежный класс элемента g
группы G по группе H
- левый смежный класс элемента g
группы G по группе H
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.