Множества и операции над ними. Отношение принадлежности. Множество. Элемент. Унификация объектов, страница 10

.

где - вес последовательности. В таком случае правило для декодирующего устройства будет иметь следующий вид:

или

Таким образом, декодер минимизирует вес оценки последовательности ошибок ê=ỹ+. Можно также сказать, что в качестве оценки  передаваемой по каналу последовательности выбирается ближайшая по расстоянию Хэмминга от полученной из канала последовательности ỹ допустимая (принадлежащая f(D)) последовательность:

В нашем курсе мы не будем рассматривать модели каналов, которые приводят к другим оптимальным правилам приема дискретных сообщений.

Рассмотрим теперь процедуру кодирования - реализации  функции f в кодере. Обычно это устройство обрабатывает входную последовательность порциями (блоками) символов и порциями символов (блоками) выдает выходную последовательность. Если результат обработки каждого блока зависит только от символов, входящих в этот блок, и не зависит от обработанных ранее блоков, код называется блоковым. Наоборот, если такая зависимость есть, код называется непрерывным.

Характеристиками двоичного блокового кода являются размеры входных k и выходных n блоков. Такой код называется двоичным (k,n) кодом. Входом является двоичные вектора размерности k (элементы V^k), а выходом - двоичные вектора размерности n (элементы Vⁿ). V={0,1}. Обычно допустимыми сообщениями являются все возможные вектора (D=V^k).

Обратите внимание, что на каждое из множеств V^k и Vⁿ с операциями поэлементного исключающего или образует алгебраические группы áV^k,+ñ и áVⁿ,+ñ, являющиеся степенными расширениями двухэлементной группы áV,Åñ, а .  Обозначим A=Vⁿ. Множество B=f(V^k)ÌA называется множеством допустимых кодовых комбинаций. Код называется групповым, если áB,+ñ - подгруппа áA,+ñ. “Сумма” любых допустимых кодовых слов также является допустимым кодовым словом в групповом коде.

Условие обратимости функции f проще всего выполнить, если все k символов из входного блока копируются в выходной, а остальные n-k символов выходного блока вычисляются по входным k символам. Такой код называется систематическим. Структура такого кодера показана на рис. 5.

Рис. 5.

Такой код однозначно задается набором n-k функций k двоичных аргументов. Вычисляемые символы называются проверочными символами блока.

Рассмотрим способ задания кода, обеспечивающий свойства группы для áB,+ñ. Для этого введем операцию “умножения” двоичного вектора на двоичную матрицу, аналогичную операции умножения числового вектора на числовую матрицу. Определение получится заменой умножения на операцию & - “логическое и” и сложения на операцию Å - “исключающее или”. Порядок перебора индексов и требования к размерностям не изменяются. В результате получаем определение для операции · :

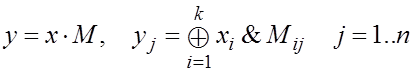
Можно проверить (аналогично числовым матрицам), что для операции · выполняется дистрибутивность относительно поэлементного “исключающего или”: (x+y)·M=x·M+y·M. Кроме того, если матрица невырожденная x·M=0 Û x=0 (0 - вектор, все компоненты которого равны 0). Эти свойства обеспечивают задание двоичного группового кода любой невырожденной двоичной матрицей, если задать y=f(x)=x·M (здесь используется представление входных и выходных последовательностей в виде векторов-строк). Такое задание называется матричным кодированием. Проверим выполнение свойств подгруппы для множества B при матричном кодировании.

1. Замкнутость:

yÎB, zÎB Þ $ x,tÎV^k: y=x·M, z=t·M Þ y+z = x·M+t·M = (x+t)·M Î B

2. 0 - нейтральный элемент в A,

0=0·MÎB

3. Обратимость:

"yÎB  y+y=0.

Систематическому коду соответствует матрица (очевидно, невырожденная) с единичной подматрицей вида:

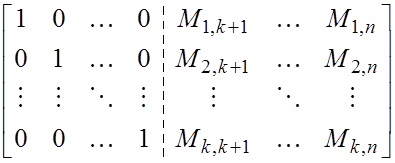
Рассмотрим структуру вычисления отдельных проверочных символов. Она задается соответствующим столбцом матрицы. Единичные элементы показывают, какие входные символы кодера участвуют в вычислении данного проверочного символа. А вычисление заключается в сложении по модулю 2. Поэтому такой код называется также кодом с проверками на четность.