Математика \ Теория дискретных структур

Множества и операции над ними. Отношение принадлежности. Множество. Элемент. Унификация объектов, страница 3

Cr - m´n, Ct - n´p

Пример: r = {(a,b), (b,b), (b,c), (c,a), (c, c)}

t = {(a,a), (a,c), (b,c), (c,a), (c,b)}

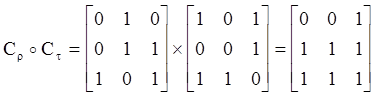
= {(a,c), (b,a), (b,b), (b,c), (c,a), (c,b), (c,c)}

 

Графическая интерпретация композиции:

3)   Обратное отношение

r-1:  rÌA´B  r-1={(x,y) | (y,x)Îr} 

4)   Степень отношения по композиции определяется рекурсивно

r1 = r

rn+1 = rn ○ r = r ○ rn

Интерпретация степени отношения: r - список всех переходов за один шаг (заданный граф)

rn - все переходы ровно за n шагов.

§4. Свойства операций над отношениями на множестве.

r, t, d Ì A2

I.  - ассоциативность

II. 

III.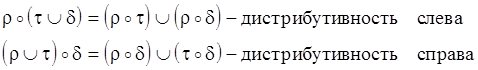

IV.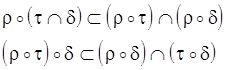

V. 

VI.

VII.

VIII.

IX.  r Ì t Þ r -1 Ì t -1

X. 

XI.

¨  Упражнение

Доказать свойства.

Пример: Ассоциативность композиции:

(x,y)Î(a∘b)∘c Û $z:(x,z)Î(a∘b), (z,y)Îc Û $z,t:(x,t)Îa, (t,z)Îb, (z,y)Îc

Û $t:(x,t)Îa, (t,y)Îb∘c Û (x,y)Îa∘(b∘c)

§5. Основные типы бинарных отношений на множестве

I. r - рефлексивно

(в графе в любой вершине петля)     ref

II. r - иррефлексивно

(в графе нет петель)    irr

III. r - симметрично

(в графе стрелки в обе стороны)   sim

IV. r - антисимметрично

(в графе стрелки только в одну сторону)

V. r - асимметрично

(в графе стрелки в одну сторону и нет петель)

VI. r - транзитивно

(в графе транзитивно замкнуты дуги)

Примеры:

1.   ²<² на R irr, асимметрично, транзитивно

2.   ²£² на R ref, антисимметрично, транзитивно

3.   r = {|x-y|£1}ref, симметрично, не транзитивно

§6. Отношения эквивалентности и разбиения.

Опр.: Отношением эквивалентности на множестве называется любое рефлексивное, симметричное и транзитивное бинарное отношение.


1)  "xÎA (x, x)Îr

2)  (x, y)Îr Þ (y, x)Îr

3)  (x, y)Îr, (y, z)Îr Þ (x, z)Îr

½½r - отношение экв. на Ai

½½(x, y)Î r - x, y - r-эквивалентны

½½


Опр.: [x]r = { y ½yÎA, (x, y)Îr}– класс эквивалентности элемента х относительно r

Опр.:{SiÌA½Si≠Æ, SiÇSj=Æ , i≠j, = A} называется разбиением множества А

Следствие: SiÇSj≠Æ Þ i=j

Пример:

r = {(x, y) | x mod k = y mod k} ref, sim, tra;   k = 5

[0] = {0, 5, 10, … } = {5m | m Î N0}

[1] = {1, 6, 11, … } = {5m + 1 | m Î N0}

[2] = {2, 7, 12, … } = {5m + 2 | m Î N0}

…

[4] = {4, 9, 14, … } = {5m + 4 | m Î N0}

N0 = [0]È[1]È[2]È[3]È[4] Þ r - разбиение N0

Опр. Фактормножество множества А по отношению эквивалентности r называется множество всех различных классов эквивалентности по r.

А/r = {[x]r | xÎA}

Теорема. r - эквивалентность на А Þ (x, y)Î rÛ[x]r=[y]r

Док-во:

1)  (x, y)Î rÞ [x]r=[y]r

z Î [x]rÛ (x, z)Î r

(x, y)Îr, (x, z)ÎrÞ (z, y)ÎrÞzÎ[y]rÞ [x]rÌ[y]r

zÎ[y]r, (x, y)Îr Þ (z, y)Îr, (x, y)Îr Þ z Î [x]r Þ [y]rÌ[x]r Þ [x]r=[y]r

2) [x]r=[y]r Þ (x, y)Îr         ||          xÎ[x]r=[y]r Þ (x, y)Îr


[x]r={y | (x, y)Îr}

[x]r=[y]r Þ (x, y)Îr

[x]r={u | (x, u)Îr}

[y]r={v | (y, v)Îr}

A=BÛ

|      xÎ[x]r т.к. (x, x)Îr (симм)

|      xÎ[x]r=[y]rÞxÎ[y]rÞ(x, y)Îr


Теорема 2. 1 Множество всех различных классов эквивалентности по r является разбиением А.

2 Отношения «принадлежать одному и тому же классу разбиения» является отношением эквивалентности на А.

Док-во:1. r - экв. на А Þ А/r - разбиение А

1)  (x, x)Îr Þ [x]r¹Æ "xÎA

2)                   

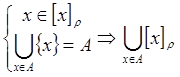
3)  [x]rÇ[y]r¹Æ Þ [x]r = [y]r

[x]rÇ[y]r¹Æ Þ $zÎA: zÎ[x]r, zÎ[y]r Þ (x, z)Îr, (y, z)Îr Þ [x]r = [z]r, [y]r = [z]r Þ [x]r = [y]r

1, 2, 3 – св-ва, опред разбиение.

2. S1, S2, …, Sn – разб. А. (x, y)Îr Û $i: xÎSi, yÎSi

1)  ref: $i: xÎSi Û $i: $i: xÎSi xÎSi Û (x, x)Îr "xÎA

2)  sim: (x, y)Îr Û $i: xÎSi, yÎSiÛ$i:yÎSi, xÎSiÛ(y, x)Îr

3)  tra: (x, y)Îr, (y, z)ÎrÞ

($i:xÎSi,yÎSi), ($j: yÎSj, zÎSj)

т.к. yÎSi, yÎSj Þ yÎSiÇSj Þ SiÇSj¹ÆÞ Si=Sj Þ

Þ $i: xÎSi, yÎSi, zÎSiÞ $i: xÎSi, zÎSi Þ (x, z)Îr

§7. Отношение порядка

Опр. Порядком на А называется любое рефлексивное, антисимметричное и транзитивное отношение r на этом множестве.

(1) (x, x)Îr  (2)  (x, y)Îr, (y, x)Îr Þ x=y   (3) (x, y)Îr, (y, z)Îr Þ (x, z)Îr

x, y - r-сравнимые Û

Если "x, yÎA  r-сравнимые, то r – линейный порядок.

Если $x, yÎA, не явл.  r-сравнимыми, то r – частичный порядок.

Система (порядок)  <A, r> - линейно-упорядоченное множество, если r - линейный порядок.

<A, r> - частично-упорядоченное множество, если r - частичный порядок.

Примеры:

1)  Отношение £ на R:  ref, ant, (x£y, y£x Þ x=y), tra (x£y, y£z Þ x£z)

линейный порядок

2)  r = min {(m, n) | n mod m = 0} = m | n (m делит n без остатка) на N (без 0)

min – ref, m | n, n | m Þ m = n  ant

(3, 5)Ïr, (5, 3)Ïr - частичный порядок.

Скачать файл