Множества и операции над ними. Отношение принадлежности. Множество. Элемент. Унификация объектов, страница 2

2.  Симметрично: A=BÞB=A

3.  Транзитивно: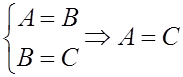

Включение

1.  Рефлексивно: AÌA

2.  Антисимметрично: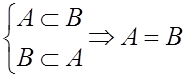

3.  Транзитивно: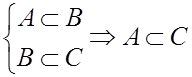

¨  Упражнение

Доказать эти свойства, используя определения.

Множество всех подмножеств некоторого множества A обозначается P(A) и определяется как

P(A)={X|XÌA}

Пустое множество не содержит элементов и обозначается Æ или {}. Условие xÎÆ всегда ложное, поэтому Æ включается в любое множество "A:ÆÌA, и как элемент принадлежит множеству всех подмножеств: ÆÎP(A). По рефлексивности включения AÎP(A). Множества Æ и A называются несобственными подмножествами множества A. Остальные, если они есть, называются собственными.

Операции над множествами:

Объединение :AÈB:xÎ(AÈB)Û  xÎA или xÎB

Пересечение :AÇB:xÎ(AÇB)Û(xÎA и xÎB)

Разность:A\B:xÎ(A\B)Û(xÎA,xÏB)

Симметричная разность:A∸B:ÎA∸BÛ xÎA,xÏB;      A∸B=(A\B)È(B\A)

или xÎB,xÏA

Дополнение: A'={x|xÏA}

Свойства операций над множествами:

1)  AÈA=A;AÇA=A - идемпотентность

2)  AÈB=BÈA;AÇB=BÇA - коммутативность

3)  AÈ(BÈС)=(AÈB)ÈС; AÇ(BÇС)=(AÇB)ÇC - ассоциативность

4)  AÇ(AÈB)=A; AÈ(AÇC)=A-закон поглощения

5)  AÇ(BÈC)=(AÇB)È(AÇC); AÈ(BÇС)=(AÈB)Ç(AÈC) - дистрибутивность

6)  AÈÆ=A; AÈU=U; AÈA'=U;  - дополняемость

AÇU=A;AÇÆ=Æ;AÇA' =Æ

6)  (A')'=A - инволютивный закон

7)  (AÇB)'=A'ÈB'; (AÈB)'=A'ÇB' - законы де-Моргана

8)  (AÈB)Ç(`AÈB)=A; (AÇB)È(`AÇB)=A

9)  RÌTÞRÈ(SÇT)=(RÈS)ÇT - модулярный закон

Свойства можно доказать, пользуясь определениями для отношений равенства и включения множеств и операций. Пример:

Доказать AÈ(BÇС)=(AÈB)Ç(AÈC):

Доказательство:

xÎAÈ(BÇС)ÛxÎA или xÎBÇС ÛxÎA или (xÎB и xÎС) Û (xÎA или xÎB) и (xÎA или xÎС)Û

Û xÎ(AÈB) и xÎ(AÈC)ÛxÎ(AÈB)Ç(AÈC):

Здесь равносильность высказываний следует понимать как одинаковость истинности всех высказываний при любых одинаковых  наборах истинности элементарных высказываний о принадлежности элемента множествам.

¨  Упражнение

Доказать остальные свойства

Декартово произведение множеств:

Определение:A´B=í(a,b)|aÎA,bÎBý - двухместное

Многоместное произведение:

A₁´A₂´¼´A_n=í(a₁,a₂,¼,a_n)| a_iÎA_i}

A´A´¼´A=Aⁿ - декартова степень A порядка n

Если A – конечно, то |A|-число элементов в A.

A,B – конечные множества:

|AÈB|=|A|+|B|-|AÇB|

(|AÈB|=|A|+|B|)Û(AÇB=Æ)

§2.  Отношения и функции.

Опр.n-арным отношением на A₁,A₂,…,A_n называется  " подмножество rÌA₁´A₂´¼´A_n

Если A₁=A₂=¼=A_nÞr - n-арное отношение на A

(n=1- унарное, n=2-бинарное,…)

Бинарное отношение на A (rÌA²)[Отношение на множестве A]

Примеры : ≤ на  R²   r={(x,y)|xÎR,yÎR,x≤y}

Способы задания :

1)  список пар

2)  матричный C_ij^r=  1,(a_i,b_j)Îr

0,(a_i,b_j)Ïr,   i=1…|A|, j=1…|B|

3)  графический

ÆÌA²®пустое отношение

A²ÌA²®полное отношение

D_A={(x,x)|xÎAÌA²® диагональное отношение

(например отношение равенства являются диагональным)

1.  (функция как отношение )

Опр:Отношение fÌA´B называется функциональным если

"xÎA  $!yÎB: (x,y)Îf

Для отношения rÌA´B

r-образом множества CÌA называется множество r(C) r(C)={yÎB|$xÎC:(x,y)Îr}

r-прообразом U на множество r^-1(U)

r^-1(Y)={xÎA|$yÎU:(x,y)Îr}

(r(A)=Er область значений r^-1(B)=D_r-область определения)

Опр.функция:

1)  f- сюрьекция (наложение),если f(A)=E_f=B

(отображение на все мн-во B)

2)  f- инъекция (вложение),если (x₁,y₁)Îf, (x₂,y₂)Îf, x₁¹x₂Þy₁¹y₂

3)  f- биекция (взаимноодназначное соответствие), если одновременно инъекция и сюръекция

Множество всех функций из A в B обозначается B^A

Для конечных множеств A,B выполняется следующая теорема

Теорема : |B^A|=|B|^|A| (a_iÎA(i=1¼|A|)Значение f(a_i) можно выбрать |B| способами)

§3. Операции над отношениями

1)   A, B - множества, r, t Ì A´B

rÈt - объединение, rÇt - пересечение, r\t - разность,  = (A´B) \ r - дополнение

В матричной форме:

C_ij^rÈt=C_ij^rÚC_ij^t; C_ij^rÇt=C_ij^rÙC_ij^t; ;

Пример: r = {(a,a), (b,b), (a,c), (b,c)}

t = {(a,a), (a,c), (b,a), (c,c)}

, , , ,

,

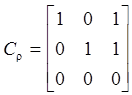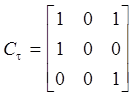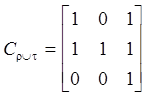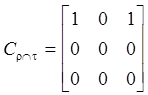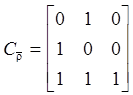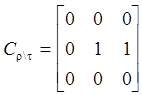
2)   Композиция отношений  r Ì A´B, t Ì B´C

В матричной форме: |A| = m, |B| = n, |C| = p