![]() - правый
смежный класс элемента g группы G по группе H
- правый
смежный класс элемента g группы G по группе H
Порядок группы ![]() .
.
Порядок подгруппы ![]() группа
группа![]() .
.
Теорема (теорема Лагранжа): Порядок любой подгруппы является делителем порядка группы, т. е.
![]()
Док-во: ![]() -
различные левые классы смежности, образующие разбиение G.
-
различные левые классы смежности, образующие разбиение G.
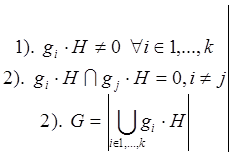 к
– это число различных левых смежных классов (индекс подгруппы Н).
к
– это число различных левых смежных классов (индекс подгруппы Н).
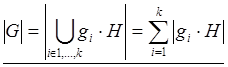 ,
т. к. различные смежные классы не пересекаются.
,
т. к. различные смежные классы не пересекаются.
Покажем, что ![]() :
:
![]()
![]()
![]()
![]()
Следствия:
1. Число различных смежных левых классов равно числу различных смежных правых классов (к) по одной и той же группе Н.
2. Порядок любого элемента группы является делителем ее порядка.
![]() -
подгруппа
-
подгруппа ![]() группы
группы ![]() .
.
![]() -
порядок элемента g.
-
порядок элемента g.
3. Если порядок группы простое число, то группа циклическая.
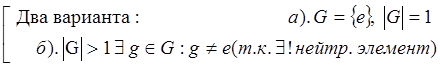
![]() делит
делит
![]() , т. к.
, т. к.
![]() -
простое число
-
простое число![]()
4. Если
![]() - простое число, то у группы
- простое число, то у группы ![]() нет подгрупп, отличных от несобственных
нет подгрупп, отличных от несобственных
![]() и
и ![]() .
.
Пример: Пример смежных классов.
![]()
![]()
![]()
![]() - подгруппа:
- подгруппа:
![]()
![]()
![]()
![]()
![]()
![]()
Смежные классы (левые):
![]() ;
; ![]() ;
; ![]() ;
; ![]()
Всего два различных: ![]() и
и ![]() .
.
![]()
![]()
![]()
Еще полезные определения:
Опр.: ![]() - группа,
- группа, ![]() -
группа,
-
группа, ![]() нормальный делитель (В
коммутативных группах все подгруппы – нормальные делители).
нормальный делитель (В
коммутативных группах все подгруппы – нормальные делители).
Опр.:
Факторгруппа:![]() ,
, ![]() -
группа,
-
группа, ![]() - подгруппа, Н – нормальный делитель
(т. е.
- подгруппа, Н – нормальный делитель
(т. е. ![]() ).
).
Рассмотрим множество сложных классов по нормальным делителям с операцией *:
![]()
Система ![]() -
группа:
-
группа:
Док-во: ![]()
![]()
Теорема: Множество всех
различных левых смежных классов элементов группы ![]() по
подгруппе
по
подгруппе ![]() образуют разбиение множества G.
образуют разбиение множества G.
Свойства разбиения:
1). ![]()
2). ![]()
3). ![]()
1. ![]()
2. ![]() , т. е.
, т. е.
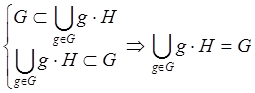
3. ![]()
![]()
![]()
![]()
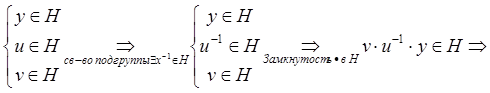
![]() , т. к.
, т. к. ![]() , т.
е.
, т.
е.
![]()
![]()
Есть аналогичные свойства для правых смежных классов.
Два элемента a и b группы G входят в один и тот же левый смежный
класс по подгруппе Н тогда и только тогда, когда ![]()
![]()
![]()
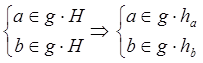
![]()
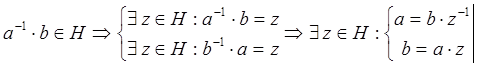 По свойству групп о решении уравнений:
По свойству групп о решении уравнений:
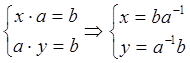
Все смежные классы образуют разбиение, следовательно
![]()
![]() , т. е. принадлежит тому же смежному классу,
что и "а", а следовательно и b принадлежит тому же классу разбиения.
, т. е. принадлежит тому же смежному классу,
что и "а", а следовательно и b принадлежит тому же классу разбиения.
![]()
![]()
¨ Упражнение
Доказать, что все циклические группы одного порядка изоморфны.
(Группа
называется циклической, если все элементы представляются в виде степеней
некоторого выделенного порождающего элемента).
Двоичные групповые коды.
Рассмотрим систему передачи двоичной информации от источника к получателю по ненадежному каналу (рис 1).
Рис. 1.
И - Источник, К - Канал, П - Получатель
Считая, что в канале нет ошибок вида пропадания или вставки символов (идеальная синхронизация) единственным видом ошибок является замена одного символа другим. В двоичном канале наличие ошибки означает замену символа противоположным (0 на 1 или 1 на 0). Замена символа на противоположный может быть выражена как результат операции “исключающее или” искаженного символа с константой 1, а отсутствие ошибки может быть выражено как операция “исключающее или” с константой 0. Поэтому такой идеализированный двоичный канал можно представить как устройство, где входная последовательность y поэлементно “складывается” (поэлементно выполняется операция “исключающее или”) с последовательностью ошибок e (рис. 2). В результате получается последовательность на выходе канала ỹ=y+e. Здесь символ + означает поэлементную операцию над двоичными последовательностями ỹi=yiÅei.
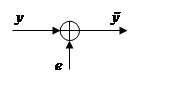 |
Для борьбы с ошибками на передающей стороне вводиться
некоторая избыточность в передаваемой информации, а на приемной стороне на
основании принятой последовательности и статистических свойств источника
информации и канала выбирается наиболее правдоподобная комбинация возможной
передаваемой последовательности ![]() и
последовательности ошибок ê. Такая схема иллюстрируется рис. 3.
и
последовательности ошибок ê. Такая схема иллюстрируется рис. 3.
 |
И - источник, КУ - кодирующее устройство (кодер), ДКУ - декодирующее устройство (декодер), П - получатель
Чтобы такая схема работала, необходимо, чтобы
зависимость y=f(x) была обратимой. Тогда![]() =ỹ+ê, а
=ỹ+ê, а ![]() =f -1(
=f -1(![]() ). Можно также написать ê=ỹ+f(
). Можно также написать ê=ỹ+f(![]() ).
).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.