2. Функции на двухэлементном множестве {0,1}
![]()
Рассмотрим операцию композиции
функциональных отношений: 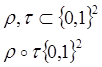
Построим таблицу ![]() (некоммутативный
моноид):
(некоммутативный
моноид):
|
0 |
f0 |
f1 |
f2 |
f3 |
|
|
f0 |
f0 |
f3 |
f0 |
f3 |
|
|
f1 |
f0 |
f2 |
f1 |
f3 |
|
|
f2 |
f0 |
f1 |
f2 |
f3 |
|
|
f3 |
f0 |
f0 |
f3 |
f3 |
¨ Упражнение
1. Найти левые и правые нейтральные элементы в этой алгебре.
2. Сколько существует различных классов бинарных алгебр на двухэлементном множестве
(Внимание, таблица 2´2 заполяется двумя значениями 16 способами, но некоторые заполнения попарно изоморфны)
Пусть ![]() -
левый и правый нейтральные элементы бинарной алгебры
-
левый и правый нейтральные элементы бинарной алгебры ![]()
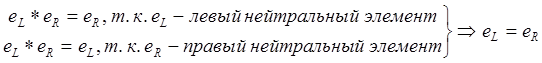
Бинарная алгебра ![]() имеет
нейтральный элемент
имеет
нейтральный элемент ![]()
Опр.:
Левым нулевым элементом называется ![]()
Правым нулевым элементом
называется ![]()
Элемент ![]() называется нулевым, если является
одновременно левым и правым нулевым элементом.
называется нулевым, если является
одновременно левым и правым нулевым элементом.
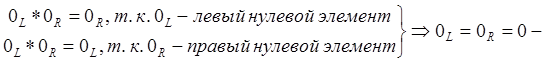 единичный
нулевой элемент
единичный
нулевой элемент ![]() .
.
Обратные элементы:
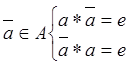
Обычно используют следующие обозначения:
![]()
![]() (нейтральный,
но не нулевой).
(нейтральный,
но не нулевой).
Теорема о гомоморфном наложении группоидов:
![]() -
Бинарные алгебры;
-
Бинарные алгебры;
F – гомоморфное наложение, если
1) ![]() - сюръективное функциональное отношение
- сюръективное функциональное отношение
2) ![]() -соотношение гомоморфизма
-соотношение гомоморфизма
В этом случае:
1. Если
в ![]() нейтральный элемент
нейтральный элемент ![]() нейтральный элемент
нейтральный элемент ![]() , причем
, причем ![]() .
.
2. Если
у элемента![]() обратный элемент, то у
обратный элемент, то у ![]() обратный элемент.
обратный элемент.
3. Если
![]()
4. Если
![]() - ассоциативна, то
- ассоциативна, то ![]() - ассоциативна
- ассоциативна
5. Если
![]() - коммутативна, то
- коммутативна, то ![]() - коммутативна
- коммутативна
Док-во:
1. ![]()
![]()
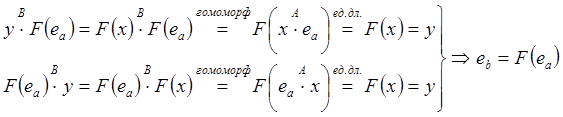
2. ![]()
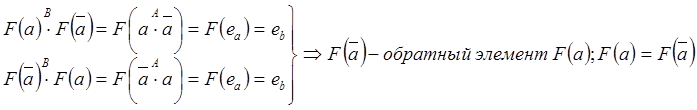
3. 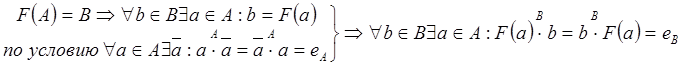 , т. е. любое b имеет обратный элемент.
, т. е. любое b имеет обратный элемент.
4. ![]()
![]() , т. к. F – сюръекция.
, т. к. F – сюръекция.
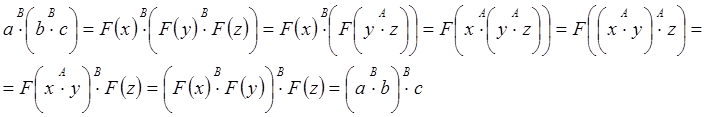
5. ![]()
![]()
Пример:
![]() ассоциативна и коммутативна, тогда
0,1 – нейтральные элементы для
ассоциативна и коммутативна, тогда
0,1 – нейтральные элементы для ![]() .
.
Если в группоиде * - ассоциативна, то существует не более одного нейтрального элемента.
Док-во:
![]()
![]()
К моноидам: (При условии, что у нас есть единичный элемент и ассоциативная бинарная операция).
Опр.: Элемент
![]() называется обратным слева, если
называется обратным слева, если ![]()
Опр.: Элемент
![]() называется обратным справа, если
называется обратным справа, если
![]()
Опр.: Элемент
![]() называется обратным , если он
обратим слева и справа.
называется обратным , если он
обратим слева и справа.
![]() Пусть
Пусть
![]() - левый обратный элемент к
- левый обратный элемент к ![]()
![]() -
правый обратный элемент к
-
правый обратный элемент к ![]()
![]() , т.
е. левый и правый обратный элементы совпадают.
, т.
е. левый и правый обратный элементы совпадают.
Пусть ![]() -
два обратных элемента.
-
два обратных элемента.
![]() , т.
е. обратный элемент единственный.
, т.
е. обратный элемент единственный.
Итог по бинарным алгебрам:
![]() -
группоид (или просто бинарная алгебра)
-
группоид (или просто бинарная алгебра)
![]() -
ассоциативна – полугруппа
-
ассоциативна – полугруппа
![]() -
моноид
-
моноид
![]() -
группа
-
группа
Также все это можно разделить на коммутативные и некоммутативные группоиды, подгруппы, моноиды, группы.
Классификация бинарных алгебр:
![]()
![]()
![]() асс.
асс.
не асс.
Условные обозначения:
-
![]() группоид
группоид
![]()
- полугруппа
-
![]()
![]()
-
![]() моноид
моноид
-
![]()
![]()
![]()
- группа
![]()
- коммутативная группа (Абелева группа)
Опр.: Группа – это моноид, в котором все элементы обратимы.
Группа – это система вида ![]() , где
, где
G – множество элементов,
· - бинарная операция
e – единичный элемент (![]() )
)
-1 – унарная операция вычисления обратного элемента
Т. о. группа – это система вида ![]() со свойствами:
со свойствами:
1). ![]()
2). ![]()
3). ![]()
В группе, как и в моноиде, единственный нейтральный элемент e; левый и правый обратный элементы совпадают. У каждого элемента существует единственный обратный элемент.
Свойства групп:
1). Правила левого и правого сокращения:
G – группа;
![]()
Док-во: ![]()
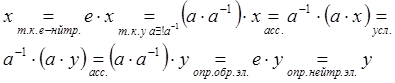
Аналогично доказывается правое сокращение.
2). ![]() - это для всех моноидов
- это для всех моноидов
3). ![]() имеет единственное решение
имеет единственное решение 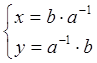
![]() ,
т.е. x – решение.
,
т.е. x – решение.
Док-во:
Если x – решение, то ![]()
Аналогично для y.
4). ![]()
Док-во:
Докажем, что ![]() – правый обратный к
– правый обратный к ![]()
![]()
Аналогично ![]()
Если
· – коммутативная бинарная операция, то
![]() – коммутативная (Абелева) группа.
– коммутативная (Абелева) группа.
Если
применить запись ![]() для
для ![]() ,
то для
,
то для ![]() используется обозначение
используется обозначение ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.