Помехи в линейном тракте АСП-ЧРК. Собственные шумы в каналах и трактах ДСП. Общие принципы анализа линейных шумящих цепей, страница 9

Измерения, проведенные на действующих магистралях, показали, что формула (9.30) правильно отражает процесс накопления мощности нелинейных продуктов второго рода, тогда как формула (9.29) оказывается справедливой только для небольших длин однородного линейного тракта, когда число однотипных НУП не превышает 10—15 [11, 16]. При больших длинах линейного тракта (при большом числе л) формула (9.29) дает завышенный результат. Такое различие объясняется тем, что при расчете накопления нелинейных продуктов участок 1—2 линейного тракта (см. рис. 9.11, а) заменялся идеальной минимально-фазовой линейной цепью с постоянной АЧХ и линейной ФЧХ. Реальные участки не удовлетворяют этому требованию,] что заставляет ставить на всех ОУП, а в системах передачи с числом каналов более 300 и на некоторых НУП (так называемых корректирующих НУП, или НУП-К) специальные магистральные (подчасточные) корректоры АЧЯ (см.  параграф  10.2).  Эти корректоры представляют собой неминимально-фазовые цепи с нелинейной ФЧХ, причем формы ФЧХ разных корректоров могут значительно отличаться друг от друга. При прохождении через корректор напряжение суммарного нелинейного продукта приобретает значительный фазовый сдвиг, который может случайным образом меняться. Это заставляет считать, что результирующая мощность нелинейных продуктов первого рода, полученная на ряде секций НУП-К НУП-К (или ОУП  НУП-К), равна сумме мощностей нелинейных продуктов отдельных секций. Следовательно, в линейном тракте, содержащем q секций коррекции, в каждой из которых имеется  НУП, результирующая мощность нелинейных продуктов третьего порядка первого рода будет равна

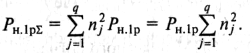
Здесь принято, что диаграмма уровней в линейном тракте, насчитывающем

усилительных пунктов, равномерна. При одинаковом числе НУП на секциях коррекции имеем  = const =иN= qn_k. Соответственно

(9.31)

Принципиально можно получить еще меньшее значение , если в пунктах коррекции установить дополнительно искажающие фазовые корректоры (ИФК) [11] , имеющие равномерную АЧХ и нелинейную ФЧХ, которая подбирается таким образом, чтобы фазы суммарных напряжений нелинейных продуктов соседних секций оказались бы близкими к . Выполнить это условие во всем диапазоне линейного спектра частот не представляется возможным, поэтому оптимизация ФЧХ ИФК производится из условия минимума суммарной мощности нелинейных продуктов в полосе линейного спектра. ИФК использую ют в системах передачи типа К-10800.

9.2.3. Распределение нелинейных продуктов в диапазоне частот

При определении спектральной плотности мощности (энергетического спектра) нелинейных продуктов предполагается, что многоканальный сигнал представляет собой сумму независимых отдельных сигналов. Каждый из них может быть рассмотрен как некоторый случайный сигнал, при этом групповой сигнал имеет нормальный закон распределения мгновенных значений. Тогда спектральная плотность многоканального сигнала G(f) и его корреляционная функция В(τ) связаны между собой преобразованием Фурье (см. параграф 1.3, формулы (1.12), (1.13)). Для группового сигнала, проходящего через нелинейное устройство, задача определения энергетического спектра сигнала на выходе  решается в последовательности: , т.е. сначала по известному энергетическому спектру сигнала на входе , используя (1.13), находим , затем определяем корреляционную функцию выходного сигнала  и, наконец, обратным преобразованием Фурье [с помощью (1.12)] находим .

Корреляционная функция безынерционного четырехполюсника с МДХ вида (9.16) определяется в виде

(9.32)

Зная корреляционную функцию на выходе, находим спектральную плотность мощности (СПМ) на выходе устройства, используя (1.13):

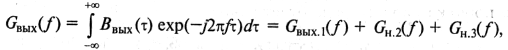
где = C₁²— СПМ полезного сигнала;

при этом G_{H 2}(f) и G_{H 3}(f) — спектральные плотности нелинейных продуктов соответственно второго и третьего порядка.