Помехи в линейном тракте АСП-ЧРК. Собственные шумы в каналах и трактах ДСП. Общие принципы анализа линейных шумящих цепей, страница 17

Расстояние между ОУП, определяемое из очевидного выражения

(9.79)

будет максимальным, если = 0. Отсюда получим уравнение

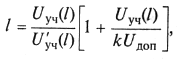(9.80)

зависит от l на основании (9.78) и (9.77). Для определения зависимости Р_{ДП 1} от l воспользуемся (9.65):

Умножим левую и правую части на и учтем (9.77). Тогда

С учетом последнего выражения решаем систему уравнений (9.78) и (9.80) при выбранном значении перекоса уровней . В итоге приходим к уравнению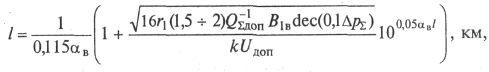

которое сравнительно просто решается графоаналитически. Найдя l, далее находим  и из (9.78) — Используя (9.79), затем определяем и максимальное расстояние i_max между ОУП.

9.3.2. Расчет мощности группового (линейного) сигнала

Во всех рассмотренных выше оптимизационных задачах предполагалось, что известен уровень средней мощности многоканального линейного сигнала  в ТНОУ. Определим эту величину для произвольного числа каналов.

Мощность многоканального сигнала в точке с нулевым относительным уровнем , очевидно, зависит от числа каналов N в тракте и средней мощности, приходящейся на 1 канал и измеренной также в ТНОУ. Чтобы найти общую мощность группового сигнала, необходимо знать, сколько в данный момент времени работает каналов, и сложить мощности сигналов в этих каналах. Если в тракте ни один канал не занят, то мощность группового сигнала будет равна нулю; максимальная мощность группового сигнала будет наблюдаться в час наибольшей нагрузки (ЧНН), т.е. в такое время, когда наблюдается максимальное число занятых каналов, хотя это и не означает, что во всех каналах одновременно идет разговор.

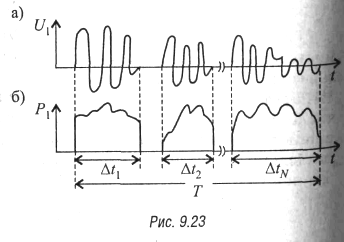
Рассмотрим изменения напряжения и мощности (рис. 9.23, а, б) сигнала в каком-то телефонном канале в зависимости от времени. Видно, что канал загружен не все время, а в отдельные моменты длительностью ,,…,Это объясняется тем, что два абонента одновременно говорить не могут (один говорит, другой слушает, и наоборот), к тому же сам характер речи, в которой имеются паузы (между предложениями, словами и т.д.), дополняет общую картину неравномерной загрузки канала. Введем понятие коэффициента активности канала , где, — отрезки «активного» времени, в течение которого сигнал передается по каналу, Т - общее время ведения разговора (занятия канала). Исследования показывают, что = 0,25  0,3, т.е. только    общего времени занятия канала используется для передачи сигнала. Обобщим эту картину на N каналов. В каждый момент времени число активных каналов всегда будет меньше N, значит, и мощность группового сигнала будет меньше максимально возможной. Мощность многоканального сигнала можно рассматривать как случайную величину. Найдем вероятность того, что в данный момент активное число каналов равно и, где п  N. Вероятность того, что активен 1 канал, очевидно, равна , а что канал неактивен — соответственно (1 - ). Вероятность одновременной активности п каналов найдем, используя выводы теории вероятностей: , где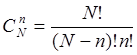 - число сочетаний из N по п.

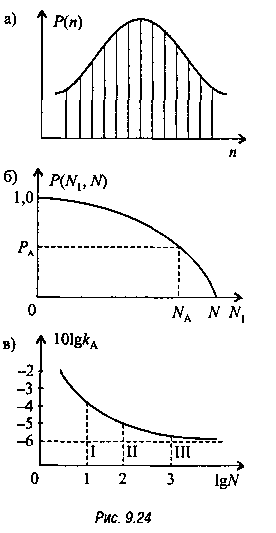
Характер изменения вероятности события «активно п каналов» в зависимости от числа и показан на рис. 9.24, а. Вероятность того, что число активных каналов лежит в промежутке (N₁,N), равна

График зависимости P(N₁ < п < N) показан на рис. 9.24, б. В технике многоканальной связи активным числом каналов N_A принято считать такое значение N₁ — N_A, вероятность превышения которого P(N_A < п < N) не более 1%. Другими словами, это означает, что в течение 99% всего времени работы число активных каналов п не будет превышать числа N_A. Значение N_A можно определить непосредственно из рис. 9.24, б, проведя прямую P_А= 0,01 параллельно оси N₁ до пересечения с функцией P(N₁ <n< N), или из приближенной формулы [48]:

Для некоторых наиболее употребительных значений N величина N_A приведена в табл. 9.2.

В таблице приведены также значения коэффициента k_A = N_A/N, показывающего относительный «вес» числа активных каналов от общего числа.