Помехи в линейном тракте АСП-ЧРК. Собственные шумы в каналах и трактах ДСП. Общие принципы анализа линейных шумящих цепей, страница 4

Защищенность можно увеличить за счет возрастания р [см. (9.12)]^ т.е. ] за счет подъема всей диаграммы уровней вверх, однако рост р, как будет показано далее, ограничивается возрастанием уровня нелинейных помех. Из (9.12) следует также, что, хотя уровень шума линии в полосе пропускания каждого телефонного канала одинаков ( = const), защищенность сигналов, передаваемых в области верхних и нижних частот линейного спектра, оказывается существенно разной. Частотная зависимость  =  является нежелательным эффектом, который необходимо по возможности уменьшить. Если выходной уровень сигнала для всех каналов в линейном спектре одинаков, р = p(f) = const, то тогда диаграммы уровней для каналов, передаваемых вблизи верхней частоты f_в линейного спектра и нижней частоты f_н, будут иметь вид, представленный на рис. 9.6.

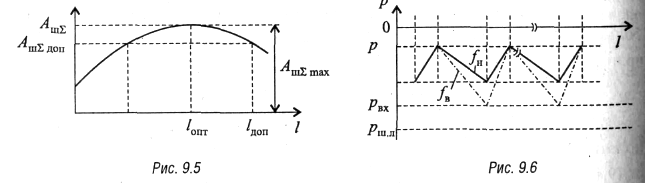
Минимальная разница между уровнями сигнала и шума будет на входе УП (рис. 9.6). Для верхнего канала эта разница меньше, чем для нижнего, следовательно, защищенность от собственных шумов в верхнем канале будет меньше, чем в нижнем .

Если принять, что коэффициент шума УП частотно-независим (d_Ш = d_Ш(f)= const), то на основании (9.12) получим неравномерность  в линейном спектре:

Обычно разница затуханий участка линии связи на верхней и нижней частотах равна 30—35 дБ. Тогда мощность шума для верхних и нижних каналов линейного сигнала отличается в 1000 раз. При этом, если выполняется норма  для верхних каналов, запас  для нижних каналов оказывается слишком большим.

Каким путем можно добиться примерно одинаковой защищенности на верхних и нижних частотах? На основании (9.12) возможны несколько путей. Первый — за счет использования частотной зависимости коэффициента шума d_Ш ⁼. При этом УП строится по схеме рис. 9.7, а, где блок 1 — частотно-зависимая пассивная цепь с затуханием a_ПЦ(f), блок 2 — усилитель с усилением S(f). Для такого варианта

где я a_ПЦ(f) = — l0lg, дБ; d_y = 101gД_y — частотно-независимый коэффициент шума усилителя 2.

Тогда при р = const [см. (9.12)]

В принципе, если Δa_ПЦ< 0 и | Δa_ПЦ | = Δa, то  = 0 и задача решена. Однако фактически входную цепь с такими параметрами использовать нецелесообразно по следующим причинам: 1) приходится существенно увеличивать усиление последующих каскадов в УП, которые компенсируют затухание линии связи и входной цепи: S(f) = a(f) + a_ПЦ (f); 2) происходит существенное снижение защищенности  для верхнего канала (см. рис. 9.7, в, где приведены два варианта входной цепи — с большой неравномерностью затухания в полосе частот а„_ц и малой а'_пц, при этом для характеристики а„_ц соответственно и большее значение на верхней частоте .

Поэтому, как правило, берется | Δa_ПЦ | < | Δa |, т.е. производится только частичная компенсация неравномерности  в диапазоне частот, причем стараются обеспечить  (см. рис. 9.7, б).

Второй путь уменьшения неравномерности  и увеличения — за счет введения предыскажения уровней по частоте. С этой целью на входе линейного тракта (выходе оконечного пункта передачи ОП₁) включают корректор предыскажений КОР₁ а на выходе последнего усилительного пункта УП_n, совмещенного с оконечным пунктом приема ОП₂, — восстанавливающий корректор КОР₂ (рис. 9.8, а). Коэффициенты передачи корректоров K₁(f)и K₂(f) подбирают так, что

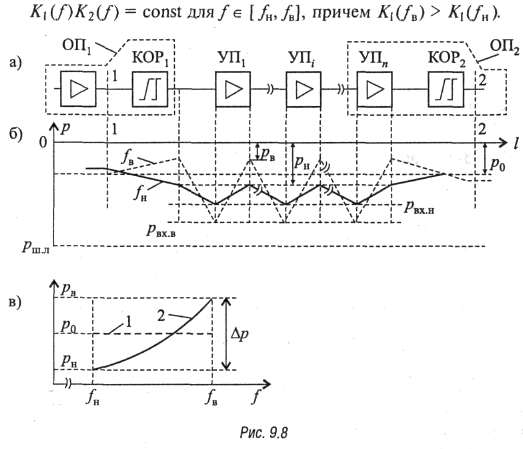
Тогда диаграмма уровней в линейном тракте примет вид, показанный на рис. 9.8, б, где и  — уровни сигнала в верхнем и нижнем каналах на выходе УП, р_о = const — уровень сигналов во всех каналах до предыскажающего и после восстанавливающего корректоров. Частотная зависимость уровней сигналов отдельных каналов p(f) на выходе УП при вве--дении предыскажений показана на рис. 9.8, в (сплошная кривая 2). Величина  называется перекосом уровней. При = 0 (при отсутствии предыскажений) имеем p(f) = р = const (пунктирная кривая 1 на рис. 9.8, в). При одновременном использовании рассмотренных выше мер (путей) получим