Помехи в линейном тракте АСП-ЧРК. Собственные шумы в каналах и трактах ДСП. Общие принципы анализа линейных шумящих цепей, страница 10

Нахождение спектра нелинейных продуктов G_{H 2}(f) и G_{H 3}(f) основано на использовании одного свойства интеграла свертки, а именно: если имеем  и известны спектры сомножителей  и , то спектр  функции произведения  определяется интегралом свертки: 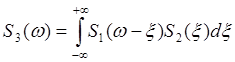(9.33)

При нахождении G_H.₂(f) можно принять

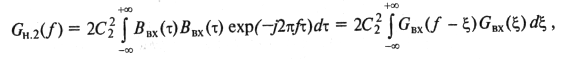
где ξ, имеет смысл текущей частоты, изменяющейся от — до +.

Используем более привычную форму записи для определения отдельной составляющей спектра нелинейных продуктов на частоте F:

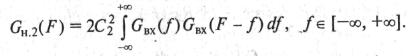(9.34)

Определим спектральную плотность нелинейных продуктов третьего порядка. Для этого, используя свойства интеграла свертки, представим

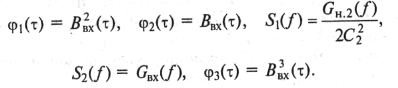
Подставляя в (9.33), получим значение спектральной плотности нелинейв ных продуктов на частоте F в следующем виде:

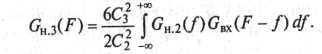(9.35)

Выражения (9.34), (9.35) позволяют определить спектральную плотность нелинейных продуктов второго и третьего порядка в общем виде. Они пригодны при любом законе изменения энергетического спектра входного сигнала  в диапазоне частот.

В качестве примера далее определим спектральную плотность нелинейных, продуктов при равномерном спектре  со спектральной плотностью G₀ в полосе f_н  f_в (рис. 9.12, а).

Используя (1.14), определим квадрат действующего напряжения группового сигнала на входе устройства

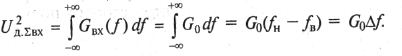
При последующих вычислениях по формулам  (9.34), (9.35) удобно полагать, чтя  — функция симметричная и определенная в области частот (—, +) в виде  = 0,5С₀H(f),где функция H(f) показана на рис. 9.12, б.

Можно убедиться, что, подставляя  в такой форме записи, получим прежнее значение . Из (9.34) для этого случая получим

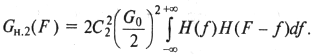
Умножим и разделим это выражение на величину, а затем учтем, что

[см.(9.20)]; = 1 мВт. Тогда оно приводится к виду

(9. 36)

Можно показать, что G_H,₂(F) и Y₂(F) — четные функции, т.е. G_H,₂(-F) = G_H,₂ (+f), Y₂(+F) = Y₂(—F). Это позволяет ограничиться рассмотрением поведения G_H2(F) и Y₂(F) только в области положительных частот (0 < F < +). Чтобы при этом не изменилась общая мощность нелинейных продуктов, учтем, что G_H.₂(-F) + G_H.₂(+F) = 2G_H,₂(F). Тогда

(9.37)

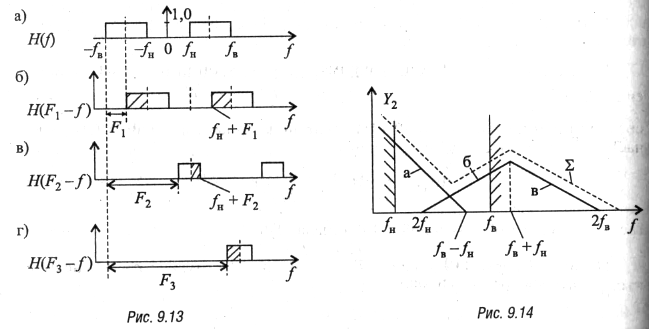
Функция Y₂(F) определяется из (9.36), подынтегральные функции H(f) и H(F—f) показаны на рис. 9.13, а, б, в, г для ряда значений F= F₁, F₂, F₃. Результат интегрирования для частот F₁, F₂, F₃ определяется площадями соответствующих заштрихованных фигур. Функция Y₂(F) состоит из трех составляющих, указанных на рис. 9.14 буквами а, б, в; каждая составляющая определяется в соответствующей области частот, причем вне ее равна нулю:

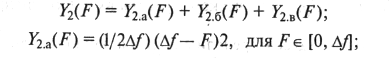(9.38)

(9.39)

Зависимость Y₂(F) на рис. 9.14 показана пунктирной кривой . Полная мощность нелинейных продуктов второго порядка на основании (9.37) определяется в виде

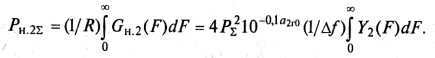(9.40)

Из (9.40) и (9.27) получим условие нормировки функции спектральной плотности нелинейных продуктов второго порядка Y₂(F)

Из рис. 9.14 видно, что некоторые нелинейные продукты не попадают в полосу пропускания полезного сигнала f_н  f_в. Для удобства расчетов вводят понятие нормированной частоты  = F - f_н /f, которая для f_н < F < f_в меняется в пределах от 0 до 1. Представляя F = f_H +  f и подставляя в (9.39), получим выражение для спектральной плотности нелинейных помех второго порядка, попадающих в полосу частот группового сигнала:

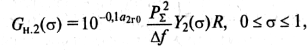(9.41

где Y₂() определяется одним из приведенных ниже выражений (9.42) в зависимости от величины  и коэффициента перекрытия частотного диапазона  = f_н / f_в

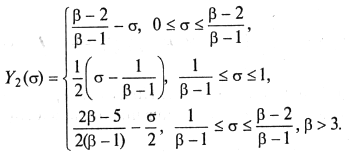(9.42)

Из графика распределения нелинейных продуктов второго порядка (рис. 9.15), построенного по выражениям (9.42), видно, что если  2, то Y₂() для всех  [0, 1] (см. также рис. 9.10). При  = 3 нелинейные продукты равны нулю только в одной точке  = 0,5. С ростом  уровень нелинейных продуктов возрастает, однако не превосходит границы, указанной на рис. 9.15 для  = .