Помехи в линейном тракте АСП-ЧРК. Собственные шумы в каналах и трактах ДСП. Общие принципы анализа линейных шумящих цепей, страница 14

2)  наименьшая общая мощность нелинейных помех второго порядка получается при обеспечении равномерной диаграммы уровней по всему тракту, т.е. при равенстве выходных уровней сигнала во всех усилительных пунктах: i⁼ Ро ⁼ const, . В этом случае суммарная мощность будет определяться из (9.61) в виде

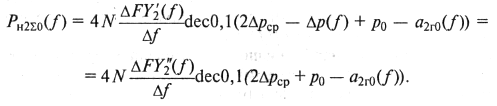(9-62)

Аналогичным образом определяется суммарная мощность нелинейных помех третьего порядка первого рода на выходе линейного тракта. Учитывая закон накопления нелинейных продуктов первого рода (9.31) и полагая, что диаграмма уровней в линейном тракте равномерна в точке с измерительным уровнем 0 дБм (ТНОУ) получим

(9.63)

В (9.63) п_К — число усилительных пунктов на секции коррекции между двумя соседними УП с магистральными корректорами.

9.3. Оптимизация параметров линейного тракта

9.3.1. Типовые задачи оптимизации ЛТ

Для систем передачи по коаксиальным кабелям помеха в линейном тракте (ЛТ) определяется суммарной мощностью собственных шумов ЛТ и суммарной мощностью нелинейных продуктов. Общая мощность помех на выходе тракта (обычно в ТНОУ) определяется как

где каждая составляющая помехи определяется соответственно из выражении (9.10), (9.62), (9.63).

Положим, что линейный тракт однороден, НУПы размещены на расстоянии /друг от друга, причем эквивалентный измерительный уровень на выходе НУП р₀, затухание нелинейности ,  и коэффициент шума d_Ш одинаковы для всех НУП. Считаем известным километрическое затухание линии связи а и полосу пропускания линейного спектра .

Под оптимальными параметрами линейного тракта понимают такие параметры, которые удовлетворяют критериям оптимальности. В зависимости от конкретных условий могут выдвигаться различные критерии. Например, при проектировании новой системы передачи критерием оптимальности может быть минимальная стоимость станционных сооружений линейного тракта; при прокладке кабеля через пустынные и малонаселенные местности критерием оптимальности может явиться максимально возможное расстояние между соседними ОУП, обеспечивающими дистанционное питание НУП; в ряде случаев важнейшим критерием оптимальности может стать наилучшее (или заданное) качество связи, которое характеризуется наибольшим (или заданным) значением защищенности от всех видов помех  в линейном тракте длиной L [16].

Рассмотрим более подробно последний критерий. Здесь под оптимальными показателями системы передачи будем понимать такие величины  = Р_опт,, L=l_опти перекос уровней  = Р_опт, при которых обеспечивается максимально возможная защищенность от суммарных помех для всех передаваемых каналов или, что одно и то же, минимально возможное отношение мощности суммарной помех!¹ к мощности сигнала. Это условие сводится к минимизации выражения

(9.64)

Поскольку соотношение помеха/сигнал нормируется для определенной длины линии связи L = l • N (обычно L = 2500 км) или на 1 км, то выражение (9.64) удобно привести к виду

(9.65)

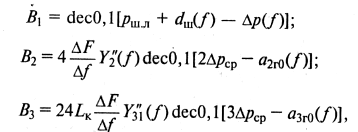(9.66)

где L_K = I п_K — длина секции коррекции, имеет смысл невзвешенной суммарной мощности помех, приходящейся на 1 км линейного тракта в точке с уровнем 0 дБм; Q₁, Q_2, Q₃,, — составляющие полной мощности помех, обусловленные соответственно собственными шумами и нелинейными продуктами второго и третьего порядка.

Из (9.65), (9.66) видно, что зависит от l, р₀, f, а также от нелинейных свойств НУП (,) и выбранного закона предыскажения уровней (при линейном перекосе — от величины ).

Если считать d_Ш, ,  известными величинами, а также задаться определенной величиной , то тогда можно считать известными и постоянными величинами [см. (9.55)] и соответственно В₁, В₂ и В₃. Тогда оптимальные значения l=l_опт и р₀= р_{0 опт} определяются из решения системы уравнений:

(9.67)

(9.68)

Система уравнений решается при . Из них следует, что при оптимальных значениях р_{0 опт} и l_опт имеем

(9.69)

(9.70)