Помехи в линейном тракте АСП-ЧРК. Собственные шумы в каналах и трактах ДСП. Общие принципы анализа линейных шумящих цепей, страница 15

Из (9.69) следует, что при оптимальном значении р_{0 опт} доля собственных шумов должна составлять от 50% (когда Q₃ << Q₂) До 66% (когда Q₂ << Q₃) суммарной мощности помех.

Из (9.70) с учетом (9.69) получаем

(9.71)

При этом а выражается в дБ/км. Учитывая (9.69)—(9.71), находим минимум  при l=l_опт и р₀= р_{0 опт}:

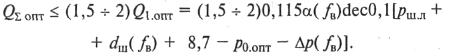
Подставляя в это выражение типовые значения, которые обычно используются в системах передачи по коаксиальному кабелю: α на верхней частоте  линейного спектра порядка 6  10 дБ/км, p_ш.л—139 дБм, d_Ш— от 8 до 10 дБ, и задаваясь значениями р_{0 опт} = - (10  20) дБ,   (5  7) дБ, получим  (5 8) 10^-2 мВт/км=(5  8)пВт/км. Для качественной связи, как будет показано  в параграфе 9.7, допустимая величина  не должна превышать  (2 6) пВт/км. Следовательно, выбор l=l_опт  из (9.71) обеспечивает слишком большой запас по защищенности от помех.

Поэтому целесообразно выбирать l>l_опт с таким расчетом, чтобы обеспечить  При этом уменьшится число НУП и снизится стоимость линейного тракта. Оптимизация параметров ЛТ в этом случае сводится к нахождению таких значений р₀, и максимально допустимой длины l_доп, при которых выполнятся условия

Аналитическое решение этой задачи невозможно из-за сложности функции , поэтому применяют метод последовательных приближений: сначала определяют область возможных значений l_доп е [l_min; l_max], потом, задаваясь рядом значений l из этой области, определяют соответствующие значения р, и , наконец, анализируя полученные результаты, выбирают наилучшие (близкие к оптимальным). Наибольшая длина усилительного участка l_мах будет в случае, когда на мощность собственных шумов Q₁ приходится 2/3 от всей мощности . При этом Q₂ << Q₃ и Q₁ = 2Q₃ . Это, как подтверждает практика, обычно выполняется на верхних частотах. Тогда из (9.67) находим оптимальный уровень:

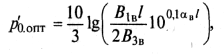(9.72).

где _В, В_1в, В_3в определяются для =.

Подставляя (9.72) в (9.65), получим нелинейное уравнение вида

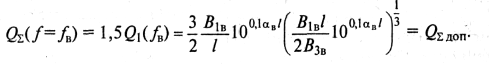(9-73)

Решение (9.73) относительно одной переменной l дает величину l _мах, а после подстановки в (9.72) и величину . Подставляя полученные значения в (9.65), находят  для . Если выполняется условие <, то можно попытаться увеличить длину участка, задаваясь большим значением перекоса уровней . При новом значении  расчет повторяют в прежней последовательности.

Если не выполняется < , то сначала пытаются добиться результата, уменьшая . Если это безуспешно, приходится уменьшать длину усилительного участка.

Минимально возможная длина усилительного участка l_min будет в случае, когда Q₂ >> Q₃и Q₁= Q₂ = 0,5; [см. (9.69)]. Из (9.67) находим

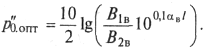(9.74)

Подставим (9.74) в (9.65) и, учитывая, что неравенство Q₂ >> Q₃длязаведомо выполняется, получим систему двух уравнений:

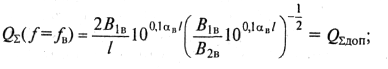(9.75)

(9.76)

где В_1н, В_2н, В_3н ,α _н соответствуют частоте.

Совместное решение (9.75) и (9.76) представляет собой достаточно сложную задачу из-за трансцендентности уравнений, поэтому ее решают с помощью ЭВМ. При этом находят l_min, Δр_опт и . При необходимости расчет оптимальных параметров продолжают, задаваясь l_mjn < l < l_max.

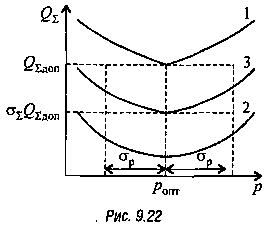
Полученные результаты проверяют подстановкой в (9.65). При этом возможны случаи, показанные на рис. 9.22 (кривые 7, 2, 3). Для упрощения рисунка минимум кривых "оказан совпадающим в одной точке .На самом деле экстремальные точки у разных кривых соответствуют разным значения Ро. Как видно из рис. 9.22, результат, представленный на кривой 1, неприемлем, так как  , на кривой 2 — также приемлем, поскольку слишком велик запас  защищенности. Оптимальный результат представлен на кривой 3, когда при р₀ =  имеем   а при р₀ =+ выполняется условие  . Коэффициент  учитывает возможное ухудшение помехозащищенности из-за разброса длин участков и неточности  установки уровней . При этом обычно = 0,7 0,8;  = ±6 дБ [16].