Помехи в линейном тракте АСП-ЧРК. Собственные шумы в каналах и трактах ДСП. Общие принципы анализа линейных шумящих цепей, страница 13

В общем случае при введении линейного перекоса уровней суммарная защищенность тем не менее будет иметь некоторую неравномерность, зависящую от частоты. Поэтому зачастую требуется введение криволинейного перекоса уровней (см. кривую 3 на рис. 9.20). При криволинейном предыскажении закон изменения уровней в средней и верхней частях спектра приближается к линейному, а в нижней части отличается подъемом уровня. К предыскажениям подобного типа относится так называемое биэкспоненциальное предыскажение, когда энергетическая плотность многоканального сигнала определяется выражением ,где ,,,— постоянные коэффициенты. Для биэкспоненциального закона возможно определение  в аналитической форме, хотя выражения оказываются достаточно громоздкими. В общем случае при криволинейном и кусочно-линейном (см. кривую 4 на рис. 9.20) предыскажениях целесообразно использовать расчет функций  и  с помощью ЭВМ.

При определении спектральных плотностей нелинейных продуктов ранее полагали, что затухание нелинейности а_2г0 а_3г0 группового усилителя не зависит от частоты. Это условие, как правило, выполняется для групповых усилителей в аппаратуре группового преобразования, которая расположена на оконечных и транзитных пунктах. В линейных усилителях ОУП и НУП для Формирования требуемой частотной характеристики усилителя используется частотно-зависимая отрицательная обратная связь (ОС). В этрм случае затухание нелинейности усилителя также будет зависеть от частоты . Если основным источником нелинейных продуктов является безынерционный выходной каскад усилителя, то при охвате этого усилителя цепью отрицательной частотно-зависимой обратной связи коэффициент усиления  и коэффициент гармоник станут равными соответственно (см. параграф 2.4)

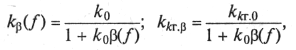
где k₀ и — коэффициенты передачи по напряжению для усилителя без обратной связи и цепи ОС.

При этом подразумевается, что при введении ОС уровень основной гармоники на выходе усилителя не изменится. Из приведенных выражений нетрудно получить

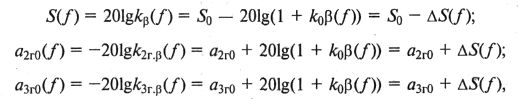
где S₀, а_2Г0 и а_3Г0 — усиление и затухание нелинейности усилителя без ОС.

Более удобно эти выражения привести к виду

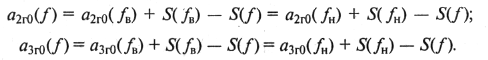(9.59)

Поскольку частотная характеристика цепи ОС такова, что  > S(f₂), если f₁ >f₂, то из (9.59) следует, что затухание нелинейности на нижних частотах линейного спектра всегда больше, чем на верхних. Это обстоятельство является полезным, так как оно в известной степени компенсирует неравномерность частотной зависимости функций и .

Проведем расчет суммарной мощности нелинейных продуктов в линейном тракте, для которого известна диаграмма уровней. Мощность нелинейных продуктов второго порядка на выходе i-о усилительного пункта на основании (9.43), (9.49), (9.59) будет равна

Обозначим  — уровень средней мощности многоканального сигнал» в точке с измерительным уровнем 0 дБм (ТНОУ). В точке х, где измеренный уровень всех каналов одинаков и равен р_X уровень средней мощности будет равен ⁼ Рх ⁺  дБм. Соответственно на выходе усилителя

(9.60)

где — эквивалентный уровень на выходе i-го усилителя во всех каналах (на всех частотах) при отсутствии предыскажений уровней.

Пересчитаем мощность нелинейных продуктов второго порядка i-го усилителя на выход линейного тракта, где уровень сигнала для удобства расчета примем 0 дБм (ТНОУ). Тогда, используя (9.55), получим

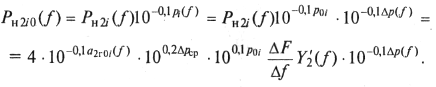
Очевидно, общая мощность нелинейных продуктов второго порядка, пересчитанная на выход линейного тракта, насчитывающего N усилительных пунктов, будет равна

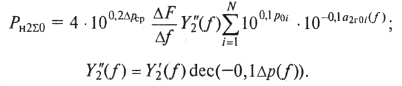(9.61)

Из анализа выражения (9.61) можно сделать следующие выводы:

1)  наибольший вклад в общую мощность нелинейных помех второго порядка вносят нелинейные продукты, возникающие на выходах тех усилительных пунктов, где имеет место наибольший по величине измерительный уровень, поэтому опасно повышать выходной уровень сигнала в усилительных пунктах выше нормы;