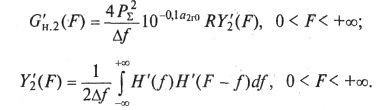Помехи в линейном тракте АСП-ЧРК. Собственные шумы в каналах и трактах ДСП. Общие принципы анализа линейных шумящих цепей, страница 12

(9.50)

Из (9.35) получим спектральное распределение нелинейных продуктов третьего порядка:

(9.51);

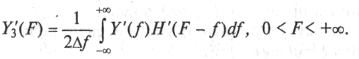(9.52)

Вывод выражений (9.49)—(9.52) производится точно так же, как и соответствующих выражений (9.36), (9.37), (9.44), (9.45) полученных для работы без перекоса уровней. Отличие заключается только в том, что при определении функций  и используется единичная функция энергетическо-1 го спектра входного сигнала с перекосом уровней , тогда как при определении функций Y₂(f) и Y₃(f) — без перекоса уровней . Методика расчета функций и  точно такая же, как и функций Y₂(F) и Y₃(f). На рис. 9.19, в приведена функция H'(F—f) произведение которой с функцией H'(f) (рис. 9.19, б) определяет  [см.  (9.50)]. Пределы интегрирования определяются заштрихованными участками функций H'(f) и H'(F-f).

Вид функций и определяется характером спектра входного сигнапа  или функцией H'(f). Удобно ввести в рассмотрение функцию, частотная характеристика которой с точностью до постоянного слагаемого ) совпадает с частотной зависимостью уровня передачи p(f): const

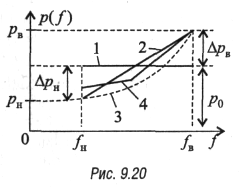
Основные варианты используемых на практике функций  и  приведены на рис. 9.20. Кривая 1 соответствует работе без перекоса уровней, кривая j 2 — работе с линейным перекосом уровней, 3 — с криволинейным перекосом j уровней, 4— с кусочно-линейным перекосом. Наиболее прост для аналитического расчета функций и вариант, соответствующий линейному перекосу уровней. Для него

где k = — коэффициент пропорциональности,  — перекос уровней; g», Рн и g_B, p_B — значения функций g(f) и p(f) на нижней f_H и верхней f_B частотах группового спектра, А/=/_в— /_н.

Определим значения ^_н и #_в исходя из условия (9.48):

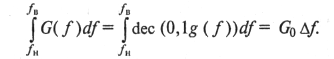
Используя (9.53) и учитывая, что decA^r= 10*= е²'^зх, получим

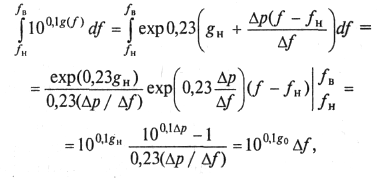
где g₀ = 101gG₀.

Отсюда, взяв 10lg от левой и правой частей, находим

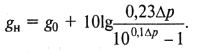
Учитывая (9.53), получим

где Ag(/) отражает отклонение распределения уровней от равномерного при введении перекоса.

Очевидно,

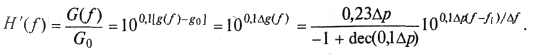
(9.54)

Поскольку функции p(f) и g(f) пропорциональны, то

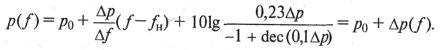(9.55)

Здесь = ,— эквивалентный уровень на выходе усилителя во всех каналах при отсутствии предыскажения уровней. Если для группового (линейного) тракта известны уровни р_Н и р_В, то из (9.55) нетрудно найти р₀:

(9.56)

Подставляя (9.54) в (9.50) и (9.52) и опуская промежуточные выкладки, получим значения коэффициентов спектрального распределения нелинейных продуктов на нормированной частоте  [11, 16]:

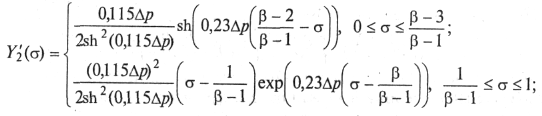(9.57)

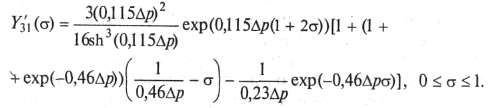(9.58)

В приведенных выше выражениях исчисляется в децибелах. Анализируя (9.57), (9.58), нетрудно показать, что при 0 эти выражения сходятся соответственно к (9.42) и (9.46). Как будет ясно из дальнейшего, удобно использовать при расчете функции и где функции и определяются из (9.57), (9.58), а функция  — из (9.55): 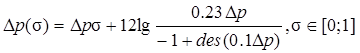 . На рис. 9.21 в качестве примера приведены значения  и  (пунктирные кривые) для нескольких значений и =3.

Анализируя распределение нелинейных продуктов, можно сделать следующие выводы:

1.  При введении предыскажений характер спектрального распределения нелинейных продуктов также существенно неравномерен и зависит от величины перекоса уровней Ар.

2.  Защищенность канала ТЧ от нелинейных продуктов зависит от его расположения в диапазоне линейных частот и от перекоса уровней. При введении предыскажений защищенность каналов ТЧ, расположенных в области нижних частот, ухудшается.

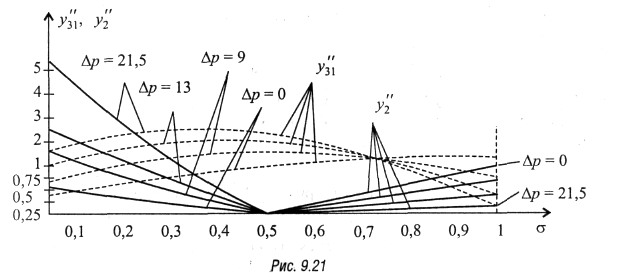
3. При введении перекоса уровней защищенность от собственных шумов выравнивается, в то время как защищенность от нелинейных продуктов становится более неравномерной. Поэтому выбирают такой перекос уровней, когда суммарная защищенность от собственных шумов и нелинейных продуктов становится более равномерной в линейном спектре частот.