Помехи в линейном тракте АСП-ЧРК. Собственные шумы в каналах и трактах ДСП. Общие принципы анализа линейных шумящих цепей, страница 7

Практически более важной задачей является такой выбор частот f_H, f_B, при котором нелинейные продукты второго и третьего порядка не попадают в полосу основных частот f_H ÷ f_B. Для нелинейных продуктов второго порядка это имеет место при выполнении условий (см. рис. 9.10): (f_B - f_H) < f_H, 2 f_H >f_B, которые сводятся к одному: 2. Для нелинейных продуктов третьего порядка указанная задача не имеет решения, т.е. при любом выборе частот f_H ÷ f_B нелинейные продукты третьего порядка попадают в спектр основных частот.

Условие  2 учитывается при выборе полосы частот стандартных первичной, вторичной и четверичной групп (ПГ, ВГ и ЧГ). При выборе линейного спектра частот МСП выполнить это условие без ущерба для других показателей системы передачи не удается, поэтому оно не реализуется. Очевидно, в этом случае в полосу линейного спектра частот попадают все виды нелинейных продуктов.

Мощности нелинейных продуктов определим, используя табл. 9.1. Предварительно определим мощность первой гармоники частоты , на выходе устройства:

(9.22)

Мощность второй гармоники частоты , на выходе устройства с учетом табл. 9.1 и (9.22) равна

Умножим и разделим это выражение на , учтем, что  / 2R = 1 мВт, и, используя формулу (9.20), получим окончательно

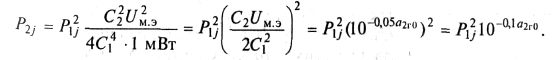(9.23)

Для 3-й гармоники Р_] = / 2R, или с учетом (9.22), (9.20)

(9.24)

Мощность -й гармонию, частоты со, определяется аналогично:

Мощность комбинационных продуктов второго порядка, используя табл. 9.1, выражения (9.22) и (9.20), определяем в виде

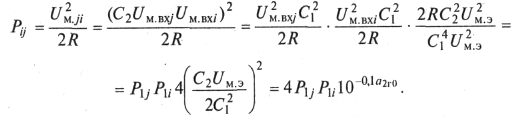(9.25)

Аналогично можно определить мощность комбинаций 2ji и jik:

(9.26)

Сравнивая (9.23) и (9.25), а также (9.24) и (9.26), видим, что мощность комбинационных продуктов существенно больше, чем соответствующие мощности ; второй и третьей гармоник. Формулы (9.22)—(9.26) пригодны также для расчета  нелинейных искажений в канале передачи.

Определим суммарную мощность N-канального группового сигнала, полагая, что канальные сигналы между собой некоррелированы и мощности основных гармоник отдельных каналов равны: ==;,[1,N]. Тогда суммарная мощность основных гармоник на выходе устройства = P_z = N. Соответственно = /N.

Для расчета суммарной мощности нелинейных продуктов второго порядка необходимо просуммировать мощности всех комбинационных частот и вторых гармоник . Учитывая число комбинационных частот и гармоник (табл. 9.1), а также (9.23), (9.25), получим

(9.27)

Таким образом, суммарная мощность нелинейных продуктов второго порядка при большом 7V полностью определяется комбинационными продуктами второго порядка.

Аналогично  определяем  суммарную  мощность нелинейных  продуктов  третьего порядка :

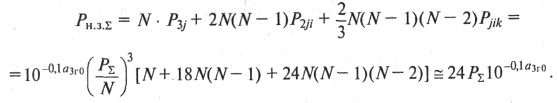(9.28)

Следовательно, при большом N суммарная мощность нелинейных продуктов третьего порядка в основном определяется комбинационными продуктами типа jik (_комб = ± , ± , ± ); j, i, k  [1, N].

Накопление нелинейных помех в групповом тракте рассмотрим на примере линейного тракта, состоящего из последовательно соединенных усилительных пунктов (УП) и участков линии связи (ЛС) (см. рис. 9.11, а). В первом приближении положим, что УП можно представить в виде последовательного соединения двух блоков, из которых первый — корректор — представляет собой линейное устройство, корректирующее неравномерность затухания участка линии связи в диапазоне линейного спектра частот, а второй блок — усилитель — представляет собой безынерционное частотно-независимое устройство, обладающее некоторой нелинейностью и обеспечивающее усиление группового сигнала до необходимого уровня. Тогда последовательно соединенные участок ЛС и корректор можно заменить линейным четырехполюсником 1—2, комплексный коэффициент передачи которого  имеет вид

Здесь  — модуль коэффициента передачи, который частотно-независим; τ — групповое время задержки, одинаковое для всех частот. Четырехполюсник с такой характеристикой не вносит никаких искажений в передаваемый сигнал, он только изменяет размах сигнала в К₀ раз и задерживает его на время τ.